Pi is 3.1446 per “Measuring Pi Squaring Phi” by Harry Lear—Reviewed

Overview

Here’s a shocking blow to the world of mathematics! A growing number of sources claim that the established value of Pi (π), 3.14159…, is incorrect. They propose instead an alternate value, claiming that Pi is 3.1446…, derived from 4 divided by the square root of the golden ratio and shown as π=4/√φ.

It seems we live in a world where truths are continually challenged, making it difficult to know what is a new discovery and what’s just fake news, click bait or a conspiracy theory.

As a recognized researcher and author on the golden ratio, these claims have naturally drawn my attention and merit a detailed response.

Among the proponents of this alternate value, Harry Lear is frequently referenced for his geometric constructions and physical measurements, which he asserts support this value at his site “Measuring Pi Squaring Phi.

This article critiques Lear’s claims, highlighting specific flaws in his assumptions and methodologies. The goal is to provide a clear, evidence-based affirmation that the traditional value of Pi remains accurate and more reliable than any proposed alternatives based on geometric constructions or physical measurements. On that note, see also my articles on a simple’s proofs of Pi’s true value via its area or circumference.

For ease of reading, the article begins with a concise explanation of all the key issues and findings. An appendix follows this for readers who wish to delve into the more detailed analysis.

Flawed assumptions in Lear’s geometric proofs for Pi is 3.1446

Lear’s foundational claim that Pi equals 4/√φ relies heavily on his first geometric proof, which he titles “Geometric Proof 1 for True Value of Pi.” While this construction is intricate and appears methodical, it contains a critical logical flaw that invalidates the entire argument.

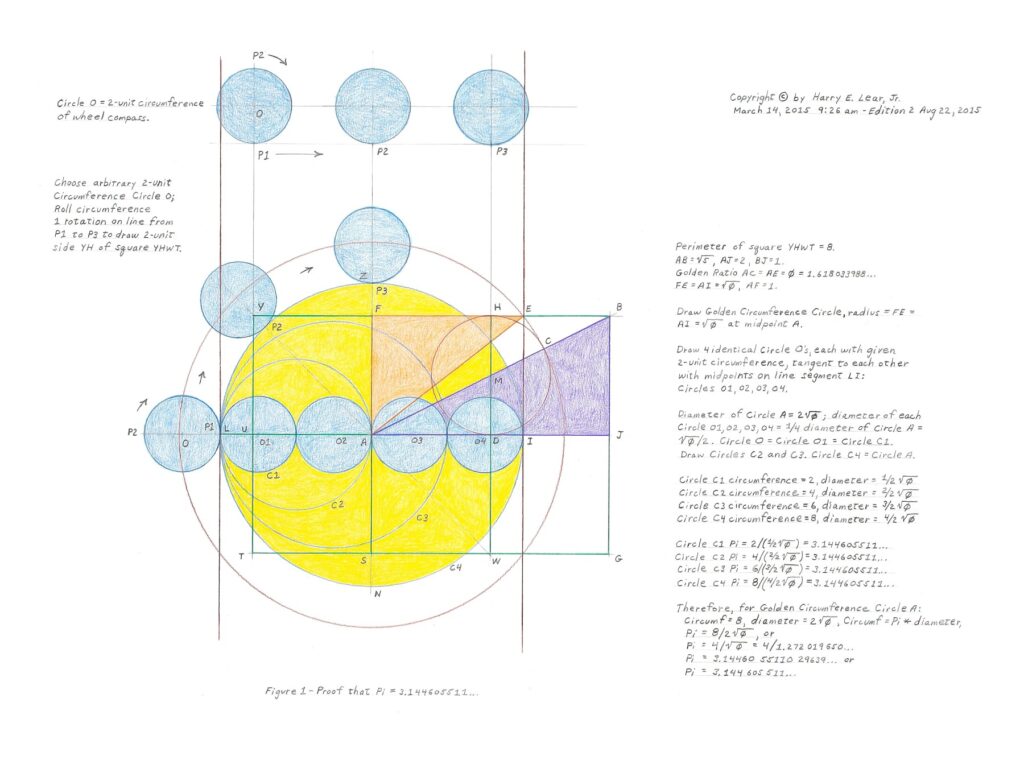
Copyright 2015, Harry E. Lear, Jr. at https://measuringpisquaringphi.com/geometric-proofs-of-pi/

In this proof, Lear constructs a circle, a line, and several geometric shapes, arriving at a line segment (LI) with a length of 2√φ (approximately 2.544039). Up to this point, the construction is mathematically valid. However, his next step introduces a critical failure. Lear states:

“Draw 4 identical circles, each with a given 2-unit circumference, tangent to each other with midpoints on the line segment LI: Circles O1, O2, O3, O4.”

The issue? Lear simply “assumes into existence” these four circles without validating their properties.

Based on the traditional value of Pi, four circles with a 2-unit circumference have diameters that sum to 2.546479…, but Lear assumes with no validation whatsoever that they all fit on line LI with 2.544039… as its length.

This step amounts to forcing his desired conclusion of π=4/√φ into the proof with no validation. How? The length of LI is 2√φ, so its quarter length is √φ/2. When Lear assumes into existence a circle with a circumference of 2 and a diameter of √φ/2, the ratio of circumference to diameter is 2/(√φ/2), which is magically 4/√φ!

This assumption is neither proven nor supported mathematically. It’s a mathematical sleight of hand that leads the reader to assume that the 2-unit circumference circle introduced in the first step must be the same 2-unit circumference circle placed on line LI. Mathematics tells us that four circles whose diameters fit on line LI must each have a circumference of 1.998083…, not 2. Ah! It’s not the same circle after all!

To illustrate how logically flawed this step is, one could just as easily “prove” that Pi equals 22/7 by constructing a line segment of length 28/11 (approximately 2.545455) and making a similar unvalidated claim that the diameters of these four 2-unit circumference circles fit to it.

Ah, and why stop there? Let’s construct a line of length 8/3 (approximately 2.666667) and we can plop these four 2-unit circumference circles on it to prove that Pi equals 3! This is great fun, but do you see the problem?

Without a mathematical validation to support this critical assumption, the entire proof collapses. Every subsequent step in Lear’s Proof 1 builds on this flawed assumption, rendering the entire proof invalid. All of Lear’s other geometric proofs also depend on this initial flawed assumption, making them equally flawed and unreliable as well.

Mathematicians have rigorously tested and validated numerous methods for calculating Pi—such as infinite series, calculus, trigonometric approaches, and Monte Carlo simulations—over centuries. These methods consistently yield a reliable value for Pi, free from the forced outcomes or limitations of unvalidated assumptions in geometric constructions.

Unreliability of physical measurements to prove Pi is 3.1446

Lear also attempts to support his claims through the physical measurements of a wooden disk. While his work may seem impressive, it too is flawed because of the inherent limitations of the materials and tools used.

CNC Tolerances and Material Limitations

A Format 4 CNC machine, known for its precision, cut the wooden disk in Lear’s experiments. However, even the most advanced machines have tolerances, and wood as a material introduces additional challenges:

• CNC Accuracy: I spoke with the technician at the CNC manufacturer. The machine itself has a tolerance of ±0.35mm, which introduces variability. He explained wood components are typically cut slightly oversized—by about 1mm—to allow for final finishing by the customer. Even with careful sanding, achieving exact dimensions is challenging. This alone could overstate Lear’s results for Pi.
• Material Properties: Lear’s choice of birch wood further complicates matters. Despite drying and precise cutting, the disk’s dimensions change with environmental humidity. Birch wood exhibits tangential shrinkage of 9.5% and radial shrinkage of 5.5%. A humidity change from 20% to 80% could cause the diameter to vary by up to 7–8mm tangentially and 4–5mm radially, significantly altering the circumference.

These factors alone make wood an unsuitable material for such precise measurements.

Measuring Tape Tolerances and Manual Errors

Lear used a high-precision Pi Tape with a tolerance of ±0.4mm to measure the disk’s circumference. While this tool is precise for many applications, it is inadequate for precisely measuring a difference of less than 1mm in diameter—the amount needed to challenge the established value of Pi. This is especially true when it is just one of several tools and processes that each contributes to overall tolerance errors.

Manual measurements also introduce additional errors. Absolutely perfect alignment and tightening of the tape around the disk are necessary for an accurate measurement. Any slack, misalignment, or surface variations will distort the measurement. These errors will always tend towards overstatement, as you can’t pull the tape tighter than perfectly.

Disk diameter inconsistencies

You can visually detect the variances in the diameter of Lear’s birch disk in his YouTube video, shown from 3:10 to 4:21 in Pi Video Diam Brand. Despite the claim that “the radius stays constant,” it’s quite clear that the disk’s radius is inconsistent and exceeds the measuring pin position many times. In particular, see the video at 3:26, 3:47, 3:59 and 4:03. Travel either over or under the exact circumference line will both increase the path and overstate the circumference and the measured value of Pi. With disk radius variations so large as to be visible to the eye, this experiment doesn’t come anywhere near close enough to the precision of 0.1% required to determine a new value for Pi.

The HDTV Simulation: An Illustrative Example

To visualize the impracticality of Lear’s measurements, consider this:

Imagine displaying a 1,000mm semicircle on a 4K HDTV screen. In the image below, one semicircle represents the traditional value of Pi (3.14159…), and the other represents Lear’s proposed value (3.1446…). Even on a high-resolution display, without the physical variations of a birch disk, the difference between these lines is nearly imperceptible to the naked eye.

Display the image below or the related YouTube video on a 55″, 65″ or 75″ HDTV and select the semicircle that corresponds to the size of your TV. That circle will have a physical width of about 1000mm, which is about 39.37″ The semicircle consists of two semicircles. The inner one in red shows the size based on traditional Pi. The outer one in blue shows the size based on Pi as 3.1446, 4/√φ. The difference between these two lines is virtually imperceptible to the naked eye.

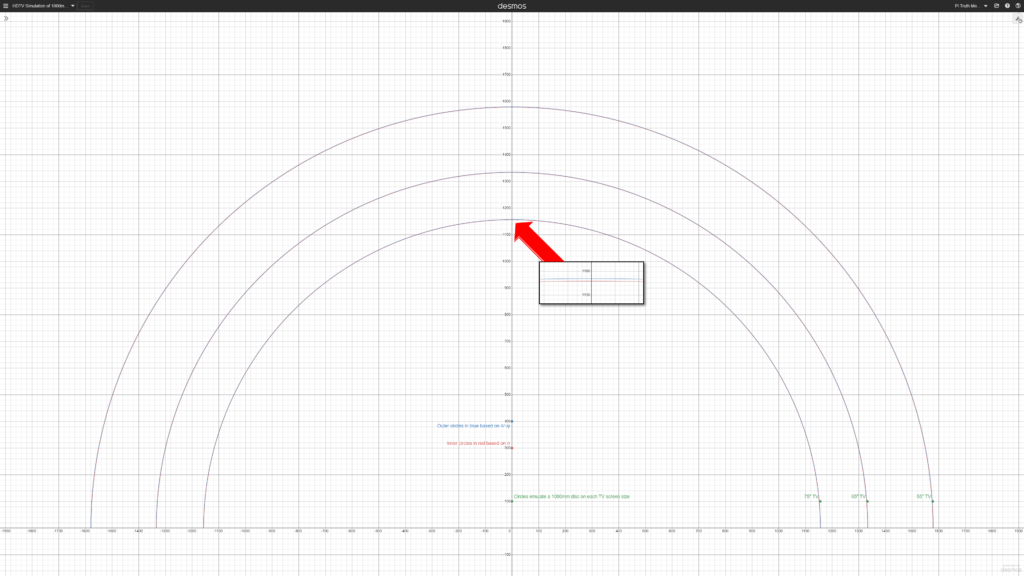
Now ask yourself: Could you accurately measure this difference with a tape measure on a wooden disk? The answer is clear—such precision is not achievable with Lear’s tools and methods.

Conclusion

While Harry Lear’s exploration of an alternate value for Pi is creative, methodical and likely sincere, his geometric proofs rely on flawed assumptions, and his physical measurements are undermined by material variability, tool tolerances, and methodological inaccuracies.

By contrast, the traditional mathematical methods for calculating Pi have stood the test of time, providing consistent and reliable results. The accepted value of Pi, 3.14159…, remains the most mathematically sound and scientifically verified.

Based on my review of other such proofs, I can state confidently that examination of every proof that claims to present a new value for Pi will contain errors in assumptions and/or methods that lead to invalid conclusions. I encourage anyone aware of or involved in these claims to stop spreading the misinformation as it is doing far more harm than good in misleading the public and in wasting the time and lives of those engaged in advocating for these proofs.

The hope of this article is to shed light on these misconceptions and reinforce the importance of rigorous proof and precision in mathematics.

---

Appendix: Detailed Analysis of Lear’s Claims

For those interested in a detailed examination of Lear’s proofs and measurements, please refer to the content below.

Introduction

The website Measuring Pi Squaring Phi with Harry Lear was created in 2017 by Harry Lear to promote this claim using geometric proofs and physical experimental evidence. It’s one of the more frequently referenced sites on this topic, with much of his work presented on a page titled Geometric Proofs of Pi.

As one who has studied the Golden Ratio since the late 1990s, I was intrigued to the investigate Lear’s claims and the evidence he provides, to assess their validity and to determine whether they offer any compelling reasons to reconsider the accepted value of Pi.

Overview

In this article, I critique the claims made by Harry Lear that the true value of Pi (π) is 3.1446… rather than the widely accepted 3.14159… value for Pi. Lear suggests this alternate value is derived from the formula 4/√φ, based on his geometric constructions and physical measurements. I review Lear’s geometric proofs and find significant flaws in their logic, which undermines their validity. The critical error lies in assuming unproven relationships between geometric figures, leading to an unsupported conclusion about Pi’s value.

Lear’s physical measurements of a CNC-cut wooden disk with a Pi Tape measuring tool are also analyzed. I identify substantial challenges and inaccuracies inherent in these methods, such as the tolerances of measuring instruments and material inconsistencies, which make it virtually impossible to achieve the precision required to redefine a mathematical constant like Pi. Through this analysis, I show that the traditional value of Pi, 3.14159…, remains the most reliable and mathematically sound constant, as corroborated by centuries of geometric proofs and physical applications.

This article aims to clarify the misconceptions surrounding these alternate claims and reinforce the importance of rigorous mathematical proof in establishing fundamental constants.

Review of Proof 1 for Pi is 3.1446

Upon reviewing Lear’s Proof 1, I found a critical flaw in its logic that undermines its conclusion that π = 4/√φ.

Proof 1 starts with a line with a length of 2, formed by the single rotation of a circle with a circumference of 2. This works, but the circle is an unnecessary assumption and an eventual diversion, as we’ll discuss later.

The proof then constructs various geometric shapes based on this line, leading to a segment (LI) that represents a circle’s diameter and has a length of 2√φ. The following steps are used:

• The line of length 2 is used to forms lines YH, UD and TW.
• From there, right triangle AJB is constucted with sides of 2 and 1, with a hypotenuse of √5.
• This hypotenuse is used to create another right triangle and other line segments with golden ratio proportions.
• Other valid steps of geometric construction lead to the creation of line segment LI (the diameter of the yellow circle) with a length of 2√φ.

The Critical Failure Point

At this point, the proof fails. Lear asserts that there are four circles, each with a 2-unit circumference and a diameter of √φ/2, perfectly fitting along line LI, saying:

• “Draw 4 identical circle O’s, each with given 2-unit circumference, tangent to each other with midpoints on the line segment LI: Circles O1, O2, O3, O4.”

However, this assumption is not proven.

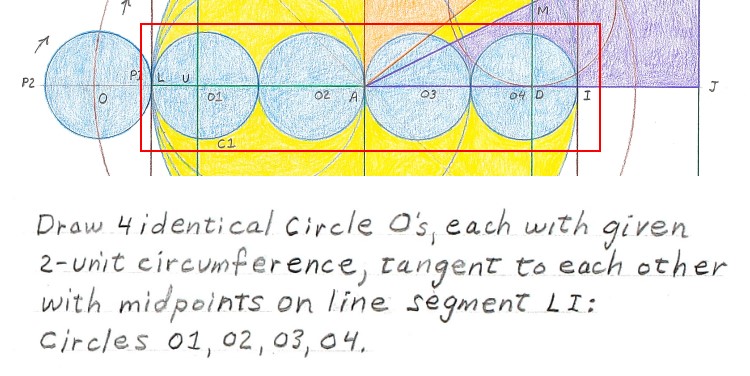
With this statement, Lear is “assuming into existence” four circles with a circumference of 2 whose diameter is √φ/2, which is 1/4 the 2√φ length of line LI.

So, out of nowhere, and with no prior proof, we now have four hypothetical circles, each with a 2-unit circumference and a diameter of √φ/2.

What’s the ratio of that circumference to the diameter? It’s 2:√φ/2, which is none other than 4/√φ, which is 3.1446…, as his presumed value for Pi. With that flaw, and this fly now in the ointment, Lear extrapolates this unproven value for Pi to draw larger circles as his “proof” of this alternate value of Pi.

Implications of flawed logic on results

With the logic and math being used here, it would have been just as meaningful, and false, to prove that Pi = 22/7 by constructing a line LI of length 28/11 and stating “Draw 4 identical circle O’s, each with a given 2-unit circumference, circumference, tangent to each other with midpoints on the line segment LI: Circles O1, O2, O3, O4.” The ratio of the circumference to diameter in this case is 2 : 7/11, and voilà we’ve just proved that Pi = 2 · 11/7 = 22/7!

There’s simply no reason to believe that the circle with 2″ circumference that Lear introduces in the first step of the “proof” to simply roll and create a 2″ line is the same circle that now perfectly fits four-abreast on line LI with a quarter length of √φ/2, or 0.636009…, as its diameter.

Until proven differently, we must assume that the correct value for Pi is still 3.14159…, and that a circle with the diameter of √φ/2 specified by line segment LI has a circumference of Pi times diameter, or π · √φ/2. This circumference is 1.99808…, not the originating circle with circumference 2, as the proof wants you to believe.

Mathematics claims demand mathematical validation

When drawn by hand in pencil, as it is on Lear’s proof, the eye can never see the difference. The “proof” is unfortunately a bit of a “mathemagical” sleight of hand, like the magician who makes a quarter “appear” from one hand while making you think it was the very same quarter that was in the other. The trick: It’s not the same quarter, nor is this the same circle.

I do not doubt Lear’s intentions, nor do I intend any disrespect. I appreciate the creativity, detailed analysis and dedication in his attempt to prove 4/√φ as the value of Pi. This, however, is simply not a proof. It’s an unsupported proposition and claim based on faulty logic.

Let’s proceed to the other proofs.

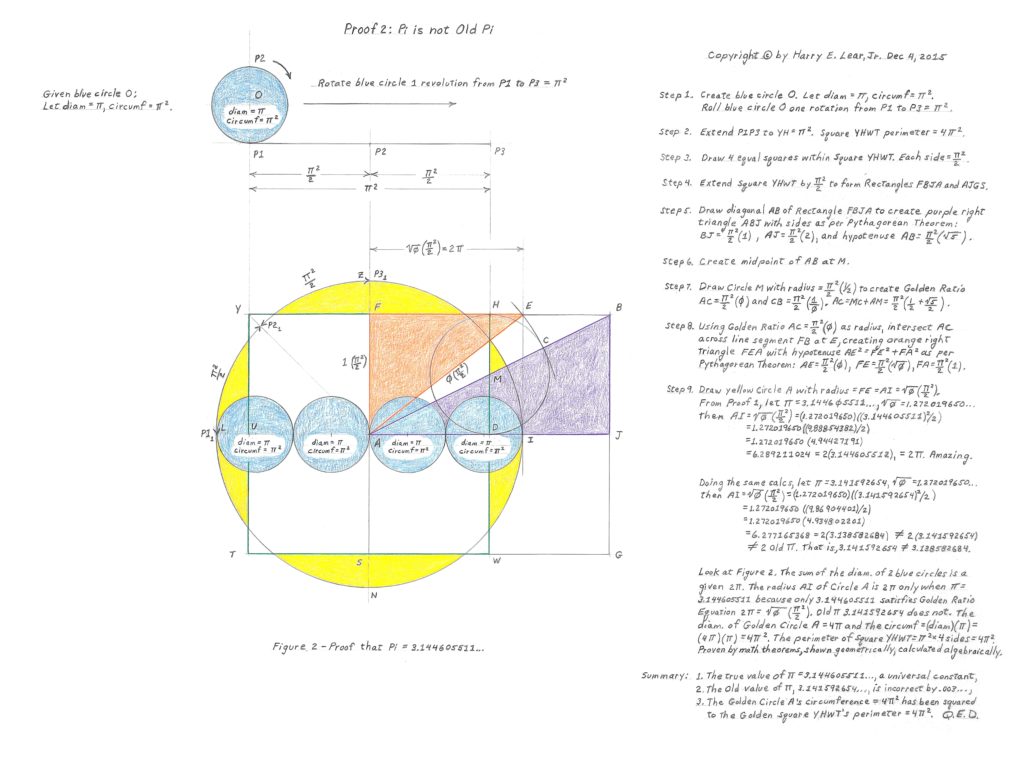
Evaluating Further Proofs

The same logical flaws appear in Lear’s other proofs. In Proof 2, he assumes π = 3.1446… based on the flawed reasoning of Proof 1, making any conclusions equally unreliable. Proofs 4, 6, and 7 also build upon these incorrect assumptions. For example, Proof 6 attempts to use physical measurements to support the value of 3.1446…, but without clear evidence or accurate methodology, these measurements can’t be trusted. The details of these proofs are as follows:

• Proof 2 – Geometric Proof 2 is essentially the same construction as that of Proof 1, appearing to be just a refinement with clearer documentation of the steps. In step 9 though, Lear says “From Proof 1, let π=3.144605512…,” and uses this to calculate the length of line segment AI with two of the same circles on it from Proof 1, concluding that they also confirm the value of 3.144605512… for π. Since Proof 1 has been shown to be flawed and false, any conclusions drawn from Proof 2 are also flawed and unreliable.
• Proof 4 – No Proof 3 is listed on the site, so we proceed to Proof 4. Step 9 says “From previous Proofs 1, 2, 3 and 5, π=4/√φ,” so unfortunately this too is based on the flawed and false Proof 1, and its conclusions are flawed and unreliable.
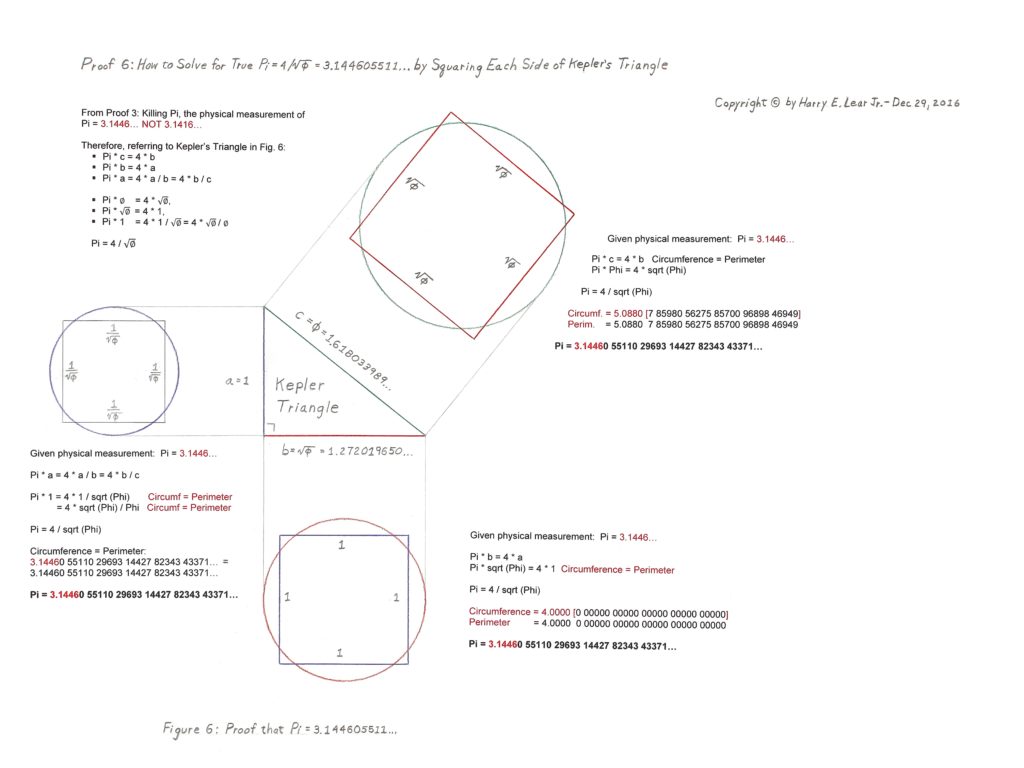
• Proof 6 – No Proof 5 is listed on this page, so we proceed to Proof 6. In the upper left corner it says, “From Proof 3: Killing Pi, the physical measurement of Pi = 3.1446… NOT 3.1416…” In the lower left, upper right and lower right of the proof, it says “Given physical measurment: Pi = 3.1446…” and then proceeds with calculations that purport to confirm the “squaring of the circle” whose diameters are derived from a golden ratio-based Kepler triangle. So here again there is no “proof” of anything, but rather just a construction that assumes Pi = 3.1446… from a physical measurement that is not clearly referenced.
• Proof 7 – Proof 7 is listed as a “Physical and Geometric Proof.” It’s based on a geometric construction from Proofs 1, 2 and 5 that has been drawn on a 40″ x 60″ foam poster board. The circle drawn on the board has a diameter of 1,000mm, and has been cut with a rotary circle cutter and beam compass. Measurements are made with a Starrett Engineering Tape Measure. In this proof, the measurements supporting Pi = 3.1446… derived from the previous flawed geometric constructions are claimed to be confirmed by physical measurement.

Physical measurements as a proof of Pi’s value

Let’s now investigate the evidence that Lear provides on the measurements he took to establish the true value of Pi. Lear continued his physical measurement experiments in 2019 on a page called “Pi Measurement.” Here he had a CNC machine “cut a 1.0000 meter diameter circle” on a wood panel.

Lear’s initial findings were based on measurements taken from a foam board disk made with a rotary circle cutter. This is clearly not at the level of that of the wood panel cut by a CNC and measured by the PiTape. It would appear that Lear recognized the obvious limitations of using a foam poster board and rotary circle cutter in getting the accuracy that is critical to this investigation, and invested in better components and processes. Accordingly, I’ll review just the evidence provided on the CNC wood panel.

Challenges of physical measurements of Pi

To evaluate Lear’s claim that Pi equals 3.1446… based on physical measurements, we first need to understand the inherent challenges and limitations involved in measuring a circle’s circumference and diameter in the real world.

The value of Pi is based on a perfect circle, whose circumference consists of all points equidistant from a fixed center point. A point in geometry is a location. It has no size, i.e. no width, no length and no depth.

Taking measurements of a circular disk in the physical world introduces these problems:

• If the disk is at all out of round, it will give a false measurement of the circumference.
• Any variances or imperfections along the circumference in the radius of the disk, whether less than or greater than the intended radius, will overstate the measure of the circumference. As illustration, “walking down into a valley and back up” or “walking up over a hill and back down” both require more steps than walking directly on a straight path.
• A measuring tape can only produce a perfect measure only if it has no thickness and is sitting exactly and directly atop the circumference. Wrapping a tape around a disk can only tend to overstate the circumference.
• A measuring tape cannot be wrapped tighter than the disc, and anything less than perfect alignment, perfect contact and perfect tightness will also overstate the circumference.

So any physical measurement is going to tend to overstate the circumference, with almost no way possible to understate it. Any physical measurement that shows the true and perfect value of Pi will require that every component and process used to be perfect as well.

Additional issues of tolerance and precision

We then must consider the issue of tolerances and precision:

• No object in the physical world will have the exact measurements that were specified for its construction. That is why manufacturers specify tolerances, such as ±0.2mm.
• High-precision manufacturing must be done with high precision components and high-precision measuring devices. A reasonable, reliable approach would be to use high-precision steel milled with high precision equipment and measured with high precision lasers. By contrast, it is not possible to achieve the same accuracy or precision when using materials like foam poster boards and wood panels, measured by hand with measuring tapes.

Challenges of using wood disks to measure Pi

Lear’s Pi Measurement page describes the experimental evidence he gathered to test his proposition that the true value of Pi is 4/√φ. Its states:

• The circular disk he used a wood disk that was cut to a 1,000.000 diameter by a $100,000 Austrian built Felder Profit H08 Format 4 CNC machine.
• He used an NIST-certified Pi Tape Corp tape measure with a cost of about $400, capable of measuring to 4,000mm.

The first thing we must do is to evaluate the level of accuracy that is possible with these components and processes. In this process we will find that the while this disk may have been specified to have a diameter of 1,000.000 mm, its actual dimension cannot be that precise and accurate. This will have a direct impact on the resulting measurement of the circumference, and conclusions on the value of Pi.

In Lear’s Pi Video Diam Brand YouTube video, he states from 3:10 to 4:21 that the video is showing that the measuring pin aligns to the circumference of the 1000 mm disk. If you watch carefully though, it’s clear that radius of the disk is extremely inconsistent. This will make any measurements taken to determine the value of Pi extremely unreliable:

Tolerance issues with precision measuring tapes

PiTape.com lists its “Precision Outside Circumference Tapes” with item #CR4MM for a circumference of 3000mm-4000mm for $488. It’s important to note from the product page that this tape has a tolerance of ±0.4mm. The standard thickness of the tape is 0.25mm.

Tolerance issues on components made with CNC equipment

The tolerances for the Felder Profit H08 Format 4 CNC machine were not readily available online, so I called their technical support line and learned the following from one of their technicians:

• The tolerance of components cut with this CNC is based on the cutting bit and how it is used..
• Wood parts will have a slight spring, and with a brand new bit will have a “give” to it.
• On wood parts, the first couple of passes must be made with a large bit, and then more passes are made with smaller bits. The Profit H08 CNC has an 8 position tool holder. A separate CNC program must be written for the pass made by each bit size, and this is critical to the results. The results thus depend on programming, and the tooling and bits used, and may not give clean edges.
• The CNC generally gets the measurements of the part to about 98% of the desired specification, leaving it oversized, with about 1mm for finishing touches. The bit will leave have small ridges that then must be finished with sanding to get to the desired dimension.
• The expected precision tolerance if all the processes are done absolutely correctly is ±0.35mm. This is confirmed by the “Conditions and Guidelines” chart he provided, which says that for workpieces larger than 400mm show that an accuracy of ±0.35mm must be expected.

The circumference of a 1000mm diameter circle with traditional Pi is approximately 3,141,592.65. If the circumference is 3,144,605.51mm, as based on 4/√φ, the diameter based on traditional Pi would be approximately 1,000.959mm.

So the determination of the value of true Pi is based on a difference in its continuous diameter of only 0.959mm. That difference can appear anywhere on the circumference and lead to an error in measurement. The tolerance errors of the disc and the measuring tape is already at 0.35mm and 0.40mm, respectively, before we even introduce the other potential errors due associated with the measurement process.

Then consider what the CNC technician said: “The CNC generally gets the measurements of the part to about 98% of the desired specification, leaving it oversized, with about 1mm for finishing touches. The bit will leave have small ridges that then must be finished with sanding to get to the desired dimension.” This means that the 1000 mm disk delivered to Lear was likely somewhat over its 1000 mm nominal size. This fact alone would lead to measurements greater the true value of Pi.

Do you see the many problems and challenges here with using physical measures to determine the value of Pi?

Seeing the challenge with an HDTV simulation of a 1000mm disc

To illustrate the challenge of accurately measuring a 1000mm disc, I’ve created an image in 4K resolution (3840×2160) showing a 1000mm semicircle. Display the image or the related YouTube video on a 55″, 65″ or 75″ HDTV and select the semicircle that corresponds to the size of your TV. That circle will have a physical width of about 1000mm, which is about 39.37″ The semicircle is comprised of two semicircles. The inner one in red shows the size based on traditional Pi. The outer one in blue shows the size based on Pi as 3.1446, 4/√φ. You may not even be able to distinguish the two separate lines.

Ask yourself this: Could you take a measuring tape and measure the red line and the blue line accurately enough to declare that one value of Pi is true and the other is false?

Conclusion on Harry Lear’s determination of the value of Pi

With respect to the geometric “proofs” of 4/√φ as the value of Pi, we find:

• Proof 1 contains a critical flaw that introduces that desired value into the construction as a mathematically unsupported and unproven assumption.
• All the other proofs either flow from the flawed Proof 1 or by interjecting an assumption that π=3.14460… There is nothing in the geometric proofs to support this value for Pi.

With respect to the physical measurements to support 4/√φ as the value of Pi, every aspect of taking such a measure can only lead to overstating the value of Pi:

• Achieving any measurement of a disc’s circumference and diameter would have to be absolutely perfect in every aspect of the construction of the disc and measurement of the disc to produce a value for Pi that agrees with its known mathematical value.
• Any variances in the disk’s diameter will overstate the distance travelled around it.
• A wood disk produced by a CNC machine is by design of the process intended to leave the disc slightly over the specified diameter to allow for fine finishing.
• Whatever the results of the measurements of a disk, they cannot be more accurate than the tolerances for manufacturing of the disc and the measuring tape.

In conclusion, the methodologies used by Lear are subject to flaws in logic and shortcomings in the capabilities of physical objects and measurement equipment.

Given the flaws in both the proofs and the physical measurements, there is nothing here that can support, by reason or evidence, that the value of Pi is anything other than the value of 3.14159… that has been corroborated by every mathematically-based proof and process ever used in modern times.

As shown by the Youtube video referenced at the beginning of this article, it is very clear that a circle can be completely covered by a quantity of squares that is less than the area it would have if the value for Pi were 4/√φ. That value of 4/√φ thus overstates the true value of Pi, and can only be false.

References

Many of the claims for π=4/√φ seem to be driven by claims of Billy Meier, but as shown in these articles even those original claims have since been refuted and reversed.

https://netpic.isgreat.ca/upload/2024/02/10/20240210115628-7310302b.pdf
https://netpic.isgreat.ca/upload/2024/02/10/20240210115627-dcb2c1fe.pdf
https://forum.futureofmankind.co.uk/d/70-pi-number/5
https://forum.futureofmankind.co.uk/u/Hush
https://www.futureofmankind.co.uk/Billy_Meier/Contact_Report_712
https://www.futureofmankind.co.uk/Billy_Meier/Contact_Report_722
https://forum.futureofmankind.co.uk/assets/files/2024-02-17/1708193263-857759-pi-e.png
https://theyflyblog.com/wp-content/uploads/2023/08/Important-information-for-the-Circle-Number-Pi-Christian-Frehner.pdf