As easy as Pi? A simple solution to a challenging problem.
With the growing number of claims on the Internet that Pi is not 3.14159… but rather 3.1446… (4/√φ), I set out to find the simplest possible way to determine which value is correct. As someone known for my work with Phi (φ), this claim, which links Pi to Phi, naturally deserved my attention.
While dozens of mathematicians, dating back to Archimedes, have already provided rigorous proofs for the value of Pi, these methods are often inaccessible to the average person. This makes it challenging for people to independently verify claims, especially when they involve complex mathematical concepts. After all, who among us—whether walking down the street or sitting in a high school math class—can confidently tackle Pi using calculus, infinite series, geometric approximations, Monte Carlo methods or Fourier series? And let’s be honest, who doesn’t love the appeal of a good conspiracy theory?
You’ll find countless claims on the Internet that attempt to “prove” Pi equals 3.14460… using intricate geometric constructions. However, for the average person, validating these claims is no easier than tackling the traditional mathematical methods. Carefully working through all the steps of these constructions, and identifying the flawed assumptions or logical errors, can take hours—if not days.
Pi = 3.14159… vs Pi = 3.1446… – A simple solution
In my other article on this topic, I used an incredibly simple approach to test the value of Pi: I drew a circle on a grid and counted how many squares it took to completely cover the circle.
This simple method only became possible with the availability of personal computing power, so it was never used by mathematicians of earlier eras.
In this model, the area based on the true value of Pi must be less than the total number of squares needed to completely cover the circle. So, an area based on any claimed value of Pi that exceeds the number of squares required to completely cover the circle must be false.
Since the difference between 3.14159… and 3.14460… is less than 1 part in 1,000, you only need a circle with a radius slightly larger than 1,000 to prove which value is correct.
You can explore the details in my article, Pi = 3.14159… vs Pi = 3.1446… – A Simple Solution, where I also provide a Desmos model and a YouTube video demonstrating how it works.
This method clearly proved that the traditional value of Pi is correct. However, even after this conclusive result, some supporters of the Pi = 4/√φ theory didn’t give up. They then claimed that there are actually two values for Pi: one for the area of a circle and another for its circumference. Let’s take a closer look at why that idea doesn’t hold up either.
Proving Pi’s relationship to Circumference and Area
Let’s tackle this from two angles: first by understanding it conceptually, and then by proving it through empirical methods.
Here’s what we already know about circles:
- The radius of a circle (r) is half its diameter (D), so 2r = D.
- The area of a circle (A) is Pi times the square of the radius, or A = πr².
- The circumference of a circle (C) is Pi times its diameter, or C = πD, which can also be written as C = 2πr.
But why exactly does the area of a circle equal πr²? Why must this be the same Pi?
The answer is actually quite simple. The area of any shape is calculated by multiplying its height by its width. If you imagine cutting a circle into very fine slices, you can rearrange these slices to form a shape that looks like a rectangle. From there, the area becomes as straightforward as multiplying height times width, just as with any other geometric shape.
This concept is beautifully demonstrated in this YouTube video by MathematicsOnline:
Area is simply Height times Width!
It’s easy to see how the rectangle we use to calculate the area of the circle is created. The height of the rectangle is simply the circle’s radius (r). The length of the rectangle comes from half of the circle’s circumference, since we divide the circle into slices with half on the top and half on the bottom. Since the circumference is 2πr, half of that is πr.
So, the area of the rectangle becomes height times width, or r times πr, which equals πr².
Conceptually, this shows that the same radius (r) is used to calculate both the area and the circumference of a circle. Therefore, the value of Pi that determines the circumference is the same value of Pi used to calculate the area.
Since Pi is used in both circumference and area calculations, it’s essential that the same value is applied consistently to both, as they are interconnected in a circle’s geometry.
That should be enough to demonstrate that there can only be one value for Pi, but let’s take it a step further and prove it empirically.
Emperical proof for π=3.14159… for the circle’s circumference
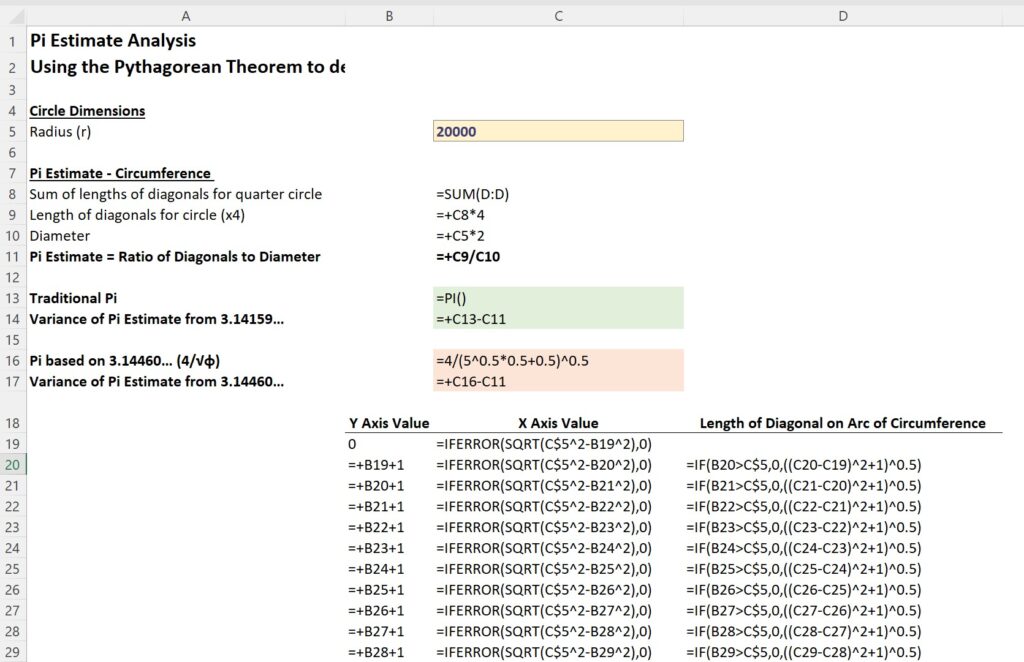
I’m still working on a way to demonstrate this using a Desmos graphing calculator model, but for now, let’s explore how we can get to the same solution and proof using an Excel model.
The model is quite simple. If you’re familiar with the Pythagorean theorem (a² + b² = c²) for right triangles, you’ll easily understand it. You can visually check the accuracy of each cell in the Excel spreadsheet by looking at the formulas or using a basic calculator.
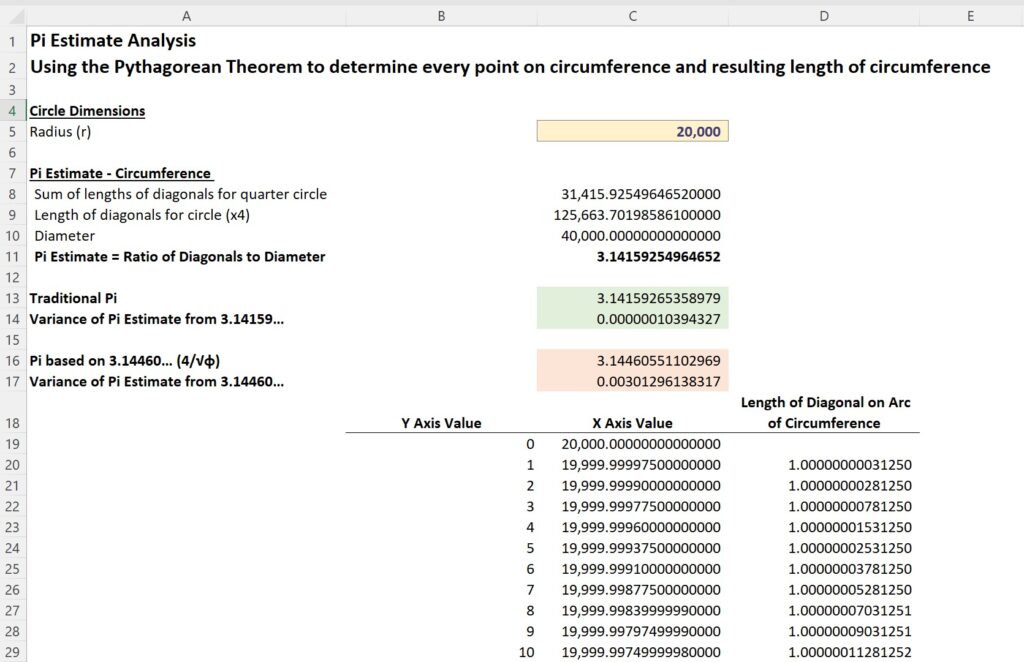
This model uses the Pythagorean theorem to calculate the x and y coordinates for every point along the circle’s circumference, based on the equation of a circle: x² + y² = r².
It then calculates the length of the hypotenuse (the line that follows the curve of the circle) for each point on the circumference, where the y-value is an integer.
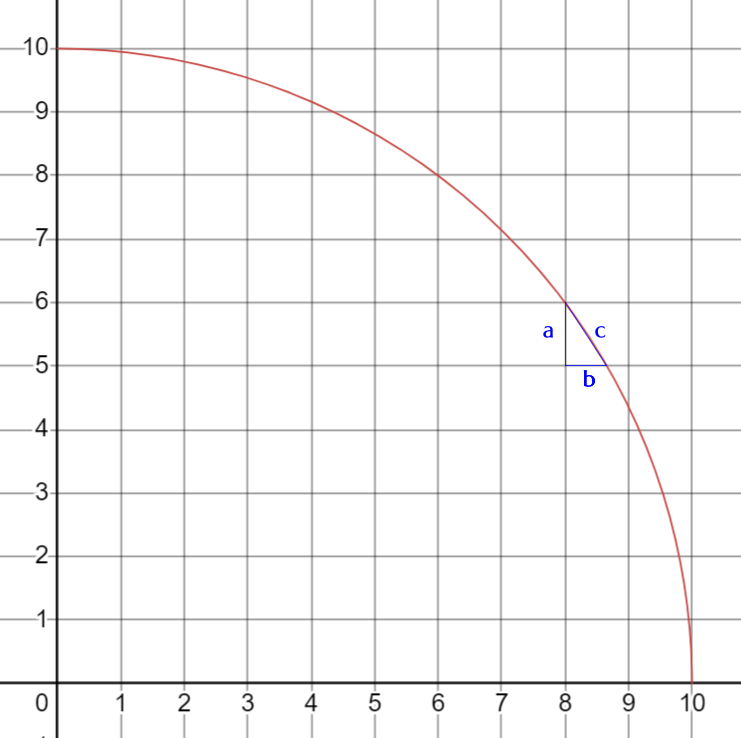
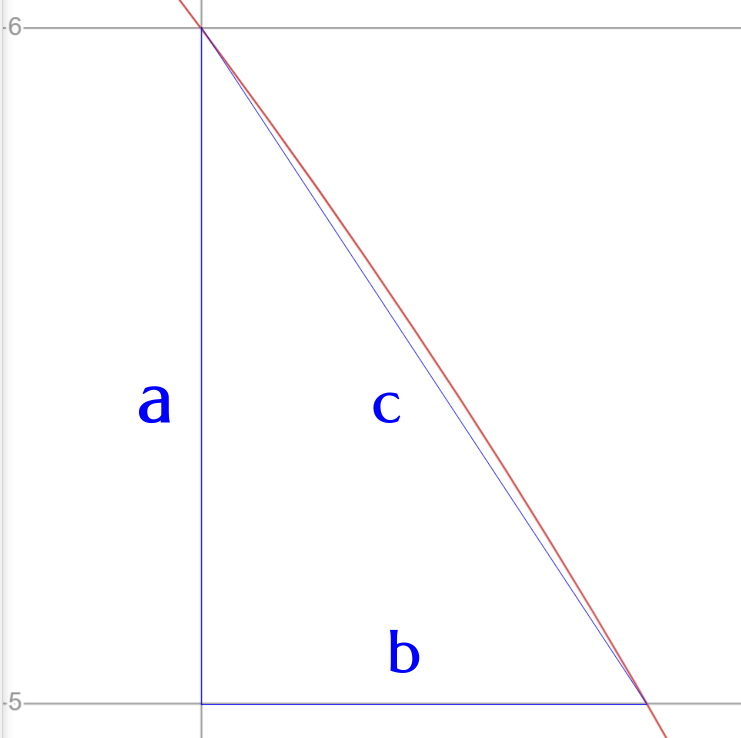
Excel’s 15 places of accuracy is more than enough
I can understand that some might say, “But that’s just an estimate, not the exact value of Pi.” And technically, you’re right—it’s an estimate. But let me reassure you that this method is far more accurate than what’s necessary to address the Pi debate.
The traditional Pi value of 3.14159… and the alternative claim of 3.14460… only start to differ noticeably at the 3rd decimal place. However, with Excel, we calculate the hypotenuse lengths to 15 decimal places, which provides an extremely precise estimate. This gives us a level of precision far beyond what’s needed to determine an accurate estimate for the circumference.
Additionally, we can make these estimates as precise as we want by using larger radii. The larger the radius, the smaller the difference between the arc of the circle and the hypotenuse used to measure it. Below are the results of the model using radii of 200, 2000, and 20,000:
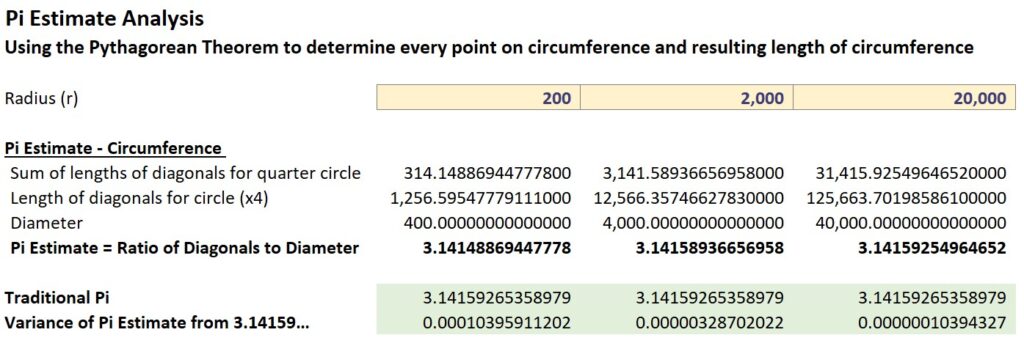
As you can see, even with the “low resolution” version using a radius of 200, the Pi estimate of 3.14148… differs from the traditional value by only 0.0001. When we increase the radius to 20,000 for higher accuracy, the Pi estimate of 3.14159… varies by only 0.0000001.
The Excel model used a radius of only 20,000 to keep the file size small. If you copy and paste the last row to extend it to a radius of 1,000,000, you’ll find that it produces as estimate for Pi of 3.14159265329582, which varies from the traditional value of Pi by only 0.00000000029398!
This level of precision offers conclusive empirical evidence that the value of Pi as 3.14460… simply cannot be correct.
The Excel model used can be downloaded here:
Pi_circumference_estimate_Excel_model_Gary_Meisner_2024.xlsx
You can also view a screen shot of the model and the formulas used here:
Moving beyond the Pi = 4/√φ myth
If you’ve been wondering whether the traditional value of Pi, 3.14159…, could be incorrect, I hope you find the simple proofs presented here helpful, easy and conclusive. You can validate it yourself: for the circumference, use the model described above, and for the area, check out the Desmos model in my article at Pi = 3.14159 vs Pi = 3.1446 – A Simple Solution. It’s important to note that neither model uses Pi in the calculations—both are based purely on applying the Pythagorean theorem to the circle’s formula.
In every proof I’ve examined for π = 4/√φ, there have been flaws—usually due to incorrect assumptions or logical errors. If you’ve been involved in supporting or developing proofs for Pi = 4/√φ, please know that revisiting these ideas is part of the scientific process. There’s no harm in learning and improving—math is about exploring and refining our understanding.
The most common mistake I’ve seen is an unsupported assumption that equates properties of squares and circles, which simply isn’t valid. The difference between 3.14159… and 3.14460… is less than 0.1%, and it’s not something you can detect with the naked eye. This makes it easy to be misled by geometric constructions, which is why verifying with proper mathematics is so important.
I understand that many people working on these proofs might not have a deep mathematical background, and that’s okay—it’s a learning process. I encourage you to review your work carefully, validate your results with well-established methods, and continue expanding your understanding of math. It’s crucial to approach this with an open mind and a commitment to accuracy.
If you still believe that π=4/φ, it’s critical to realize this:
You can’t just do a geometric construction or even a physical measurement that you claim proves your case. You have to explain why every other method ever used to calculate the value for Pi failed. Calculus, infinite series, Monte Carlo simulations and other mathematical methods are used in countless industries for countless applications and all produce accurate results wherever they area applied. How can these methods get it right for every other problem to which they are applied, yet fail for something as simple as the value of Pi? How can that make any sense? Move beyond the concerns about the accuracy of Archimedes and his polygons and take on Newton and calculus and the fact that we can now create very simple computer programs and spreadsheet models that show the value of Pi to 15 digits within a few minutes from our home computers. How can you show the failings in all of these other methods?
As for those influenced by claims that physical measurements show Pi to be something other than 3.14159…, it’s important to recognize that such small differences require extremely precise equipment. Basic measurement tools used in these “proofs” aren’t sufficient to challenge centuries of work, especially when multiple mathematical approaches all confirm the same value for Pi.
It’s time to move beyond the idea that π = 4/√φ and direct our energy toward projects that deepen our understanding and lead to meaningful discoveries.



It’s depressing that people are arguing about the value of this fundamental number after it was established thousands of years ago. That doesn’t say much for the education level of some of our fellow citizens, or their trust in knowledge rather than magical thinking (and for that matter blatant lies). These days problems dealing with facts may be evident in other ways too….
I began to read your article until I realized that you’re just working with straight lines to approach the length of a circular one. Then I stopped.
This way of approaching π yields unavoidably 3.1425926…..
You could have used any other known method and spare your time.
*The most common mistake I’ve seen is an unsupported assumption that equates properties of squares and circles, which simply isn’t valid.*
To obtain π=3.1446 I used the equality 4b=π.
It means a Square with the same perimeter as the basic circle of diameter 1.
Is this an „unsupported“ assumption?
There are no Squares with the same perimeter as a circle?
Are you saying that?
*The difference between 3.14159… and 3.14460… is less than 0.1%, and it’s not something you can detect with the naked eye. This makes it easy to be misled by geometric constructions, which is why verifying with proper mathematics is so important.*
We don’t use Geometry to guess by sight!
It is the geometric construction, the proportions that we obtain that contain the values we’re looking for.
You don’t use the ruler in geometry to „measure“ your results!
Besides, the value 3.1415926…is not incorrect.
It is correct regarding the method you use to obtain that value, which is nevertheless an approximation.
What the exact value of π=3.1446…. proves is, that to measure Space with a circular or a straight line yields not the same result and differs by +–0.003 of the diameter. And this is a significant move towards a better understanding of Math and Physics.
I can’t understand why are you so stiff against 3.1446. And so much so, that you make conceptual mistakes yourself.
The concern about the use of straight lines is why my first proof was far simpler yet. See my article at Pi = 3.14159… vs Pi = 3.1446… – A simple solution. This solution evaluates the very simple question: How many unit squares does it take to COMPLETELY cover a circle. The Desmos model is a precision digital representation of a physical experiment that you could do in the real world, and is based entirely on integers. No approximations. Just a count of squares. It too shows conclusively that an area based on π=4/√φ OVERSTATES the actual area of the circle. No guessing. No estimating. No approximating.
The cirumference proof in the Excel model produces an estimate, but with far more precision than is needed to prove that 3.14460… CANNOT be the true value of Pi.
Just because you use geometry doesn’t mean that your construction is accurate or correct. As you note, “the proportions we obtain contain the values we’re looking for.” Your geometry needs to be validated by math, but none of the geometric solutions attempt to do that.
Please go back an look at every step in your construction and identify where you’ve made a flawed, unsupported assumption or error in logic.
Further, there is a geometric demonstration of π 3.1446.
Google it: „Das Geometrische π“
And, being geometry, it is based on theorems, not on a direct measure with the ruler. Ok?
“Based on theorems” doesn’t automatically produce truth. Please see my initial proof at Pi = 3.14159… vs Pi = 3.1446… – A simple solution as it conclusively proved that π=4/√φ OVERSTATES the area of the circle.
*“Based on theorems” doesn’t automatically produce truth.*
Theorems are certainly mathematical truths, established as stereotypes so you don’t need to calculate them always from the beginning.
They are tools and if you use them correctly your result will be correct as well.
*Please see my initial proof at Pi = 3.14159… vs Pi = 3.1446…– A simple solution as it conclusively proved that π=4/√φ OVERSTATES the area of the circle.*
Archimedes has done already a similar job, calculating the lower and the upper limit of the π value and yes, 3.1446 excedes the upper limit. But it still is an approximate value obtained by adding segments of straight lines.
As I told you many times already, using straight line segments to approach the circular perimeter of the circle, this will give you always the same value, namely: 3.1415926….and whatever the amount of decimals you calculate it is still and always an approximate value
But, if you have a method to calculate the perimeter in an exact way, in one step and not in many, then you obtain 3.1446…whatever the reason.
*Just because you use geometry doesn’t mean that your construction is accurate or correct.*
Of course it doesn’t.
I didn’t use basically geometry but an algebraic solution, which nevertheless can be corroborated geometrically.
But here is a link to a pure geometrical solution for the π value. Please go there and tell me then what is wrong about it. (it is in German but you can surely stick it in a translation software)
“Das Geometrische π”
*As you note, “the proportions we obtain contain the values we’re looking for.” Your geometry needs to be validated by math, but none of the geometric solutions attempt to do that.*
The geometry is a validation in itself, because it gives you the values you’re looking for.
Based on your statement, it appears that you do not understand my area model with the YouTube video and Desmos model.
The area model does NOT use straight lines to APPROACH circular perimieter of the circle or to APPROXIMATE the value of Pi.
The model simply does an integer count of the number of squares on on a grid it takes to COMPLETELY cover the circle. Certainly you would agree that a 1″ diameter circle can be completely covered by a 2″ square, i.e. by 4 1″ squares. The model just refines that same concept.
The model doesn’t even try to approach the circumference to estimate Pi. To the contrary, as I show in the closing minute of the YouTube video, the alternate formulas provided go well beyond the number of squares required to cover the circle. We can keep on covering more and more squares and still show that it can be done with a lesser area than is computed based on πr² when π=4/√φ.
Simply stated, the area of the circle as calculated by πr² when π=4/√φ produces a number that EXCEEDS the area of the integer number of unit squares that more than completely covers the circle, which of course is greater than the area of the circle itself. Therefore 4/√φ cannot possibly be the correct value for Pi.
*Simply stated, the area of the circle as calculated by πr² when π=4/√φ produces a number that EXCEEDS the area of the integer number of unit squares that more than completely covers the circle, which of course is greater than the area of the circle itself. Therefore 4/√φ cannot possibly be the correct value for Pi.*
Simply stated too, if you’re using a circle with a perimeter = π = 3.1415926, of course the area of a circle of perimeter 3.1446 will be bigger!
You always consider π to be 3.1415926 and the program you use todo the trick is programed the same way too.
A veritable „circular“ reasoning.
There is no circular reasoning here. The formula for a circle is x²+y²=r². That doesn’t embed or rely on any particular value for Pi.
My area model on Desmos shows the exact integer number of unit squares on the grid that must be colored in to completely cover the circle beyond its perimeter. That doesn’t rely on any particular value for Pi.
So how does this imply that I’m using a circle with a perimeter of π=3.1415926… unless that is in FACT its value?
Please examine my area model and see if you can identify anything at all that is wrong with it. It’s so simple:
1) Draw a circle on a grid.
2) Color over the squares on the grid required to completely cover the circle.
3) Count how many full squares it took to do it.
4) Calculate the area of the circle using πr² for traditional Pi and 4/√φ to see which one fits inside the area of the squares you just counted. Only traditional Pi works, once you get past a radius of about 1,500 which is required to distinguish between the small difference in the two values of Pi.
Try it first with some graph paper, a compass and a pencil to validate it, or watch the video showing the examples from a small radius to larger ones.
There is absolutely NO use of Pi required to do this, so there can be no inherent bias in the result. You’re making a false assumption about the value of Pi being embedded and not understanding how simple this really is.
If you want to communicate your proof to readers, please provide an actual link to the document in English rather than asking people to Google to find it and then translate it themselves.
Here is the Link, which I got in a matter of a second after tipping „Das Geometrische π“. The value obtained is 3.1446……
And I will warn the author to write to have it translated in english…ASAP.
Ok.
https://3.141592653589793238462643383279502884197169399375105820974944592.eu/wp-content/uploads/2017/09/Geometrisches-Pi.pdf
ChatGTP knows German so I asked it to evaluate this “proof” and present its findings in English. The results are here:
Geometrisches_Pi-Review_by_ChatGTP_2024.pdf
We don’t have to go past the subtitle of the article though to see that this “proof” is comical and useless in determining the true value of Pi.
The subtitle is:
π geometrisch ermittelt als Gerade im Thaleskreis (mit 99,9%iger Genauigkeit), or
π determined geometrically as a straight line in the Thales circle (with 99.9% accuracy)
If this method produces a value with 99.9% accuracy, it’s range of error is as follows:
Stated value = 3.14460…
Lower value at -0.1% = 3.14146…
Upper value at +0.1% = 3.14775…
So the traditional value of Pi at 3.14159… falls WITHIN its stated margin of error!
This “proof” thus does NOTHING to disprove 3.14159… as the TRUE value of Pi.
We could use 22/7 as the value for Pi and also achieve 99.9% accuracy, but what does that prove???
There was no link included in your post. If you want to communicate your proof to readers, please provide an actual link to the document in English rather than to translate it themselves.
Lovely effort for order and accuracy.
Why do you need so much time to approve a comment?
It isn’t politics, it is just math we’re talking about.
I moderate all comments to assure the overall quality of the site. Without that, many sites degrade into worthless content and degrading comments.
If it’s just math we’re talking about, why do those who claim that π=4/√φ not use mathematics to validate the results of their geometric constructions? What we’re actually talking about here is truth and the use of mathematics and science to uncover it and support it. I would truly appreciate meaningful dialog on the circumference-based model I’ve presented on this page and the area-based model at Pi = 3.14159… vs Pi = 3.1446… – A simple solution. Are there any flaws that exist in the methodology, and if corrected how do they support π=4/√φ?
Saying the “it uses lines” isn’t a valid objection when the results are accurate to 9 decimal places, and no one has yet to explain why my area-based model isn’t a conclusive proof that π=4/√φ is false. See https://youtu.be/9Z9yfLMvAJQ.
Now, tell me what is wrong in this demonstration:
We take a square and a circle of the same perimeter π and write the equation
4b = π
We calculate the areas, using 4b for π, for the area of the circle.. Respectively we obtain :
As = b^2
Ac = b
Now we use these values as the legs of a right triangle to apply Pythagoras and find out the value of b or π/4.
(b)^2 + (b^2)^2 = 1
b^2 + b^4 – 1 = 0
b = 0.7861513
4b = π = 3.1446
The reason to take the Hypotenuse = 1 is simple. The value of b and b^2 are calculated for Diameter = 1.
So, the only semicircle where we can inscribe this right triangle to preserve the values of b and b^2 is one of Diameter = 1
Tell me now where is the mistake in this derivation.
To make the evaluation of your claim quick and unbiased, I entered the following text in ChatGTP. I use it regularly and have found it to be incredibly brilliant and analysis and documentation. It can even create complete working computer code from a simple prompt providing a simple description of the application. See the results below:
INPUT TO CHATGTP:
Please evaluate this claim for a proof that Pi is equal to 3.14460… and provide a response as to its accuracy or fallacy.
I then pasted your comment exactly as it was written.
HERE IS THE RESPONSE FROM CHAT GTP:
I hope you’re not paying fees to use the CHAT.
The amount of nonsense written by this program is overwhelming.
First off:
b is not an unknown! It is π/4.
2nd.
Ac=b.
b is not equal to the circumference but to 1/4 of it.!
The program considers b to be an unknown, which is more than wrong.
3rd
Pythagoras does not apply exclusively to lengths but to VALUES! And we represent those VALUES through the length of the sides.!
Resuming:
The whole text of the CHAT is wrong.
Simply because it didn’t check that b=π/4 and it relates the whole reasoning considering from the beginning that π equals 3.1415926.
Either is the program insufficiently provided with data or you didn’t feed it with the needed information.
…and now, please….give your own conclusion.
Perhaps the brief text you provided to describe your proof wasn’t adequate to provide a clear definition for its evaluation. In any event, keep in mind that even ONE false assumption or error in logic is enough to make your proof invalid. To do this kind of geometric proof you need much more rigor, like that provided by Euclid in Elements, which was the foundation of geometry text books for ages.
It’s easy to make a mistake in a long, complicated proof. The extremely simple concept of my area proof though is incredibly easy to see visually, validate with a number of sample input values and to distinguish which of the two values for pi is correct.
Ok. Using your method you draw a circle.
Well. How do you know if this circle has a perimeter 3.1415926 or 3.1446?
When you draw the circle you don’t know. The circle’s formula is x²+y²=r² so this has nothing inherently to do with the value of Pi.
You just draw the circle on the grid, color the full squares required to COMPLETELY cover it and count the squares. This gives you an integer number that defines an area which MUST be larger than the area of the circle itself.
From there you use Area=πr² to determine if traditional Pi or 4/√φ produces an area that is less than the count of the squares. As the model shows, 4/√φ FAILS this test for every value of r greater than 1,500.
A radius value greater than 1,500 is needed simply because the difference between the two values for Pi is less than 1 in 1,000. You need enough resolution to see the difference in the results.
If you do this on paper you don’t even need to know the formula for the circle, or its perimeter value.
Just draw, color and count. It’s really that simple.
*When you draw the circle you don’t know.*
You can’t do that.
As soon as you draw a circle you have already the real value of π, even if you don’t know it yourself.
The colored squares are also in a fixed relationship with that unknown value of π.
This being said, you can’t just apply arbitrarily some value you want to check up and compare the next with it. It doesn’t work like that.
You’re correct that the REAL value of π is defined by the circle and its radius.
There is nothing arbitrary about this. The formula of the circle and its physical are clearly defined. The unit squares on the grid are clearly defined. The act of coloring the full unit squares needed to completely cover the circle is a task that we could assign to an 8 year old. Nothing arbitrary about that either. Counting them wouldn’t require much higher academic skill.
NO arbitrary value was assigned. Where do you see that in the model? The integer number of squares that required to cover the circle with radius r is obervable, quantifiable and distinct.
Yes, it does work like that. How could it not?
You don’t know the real value so you can’t just choose one arbitrarily to test your method.
In other words, whatever value you take, not knowing the right one, is arbitrary and doesn’t prove anything.
You’re just guessing to prove something you have already in mind.
Just look at your picture and consider for a moment to be 3.1446 the real π. Then you understand what you’re really doing. You can’t miss it.
You can’t just “consider” 3.14460… to be the real π. Why would you think that? The circle has only ONE true value of Pi. It’s area can be only ONE true value for a given radius.
The area that COMPLETELY covers the circle must be greater than the area of the circle itself. The area based on πr² when π=4/√φ EXCEEDS even that number so it logically cannot be the true value for Pi.
My model does not “CHOOSE” or “CONSIDER” a value of Pi. It just draws a circle.
How did I “GUESS” something? Nowhere in the model does that happen. The numbers speak for themselves. That’s what mathematics does.
*The subtitle is: π geometrisch ermittelt als Gerade im Thaleskreis (mit 99,9%iger Genauigkeit), or
π determined geometrically as a straight line in the Thales circle (with 99.9% accuracy)*
*If this method produces a value with 99.9% accuracy, it’s range of error is as follows:*
This has another meaning.
The author is most probably an academic and wants to cover himself against the wrath of his colleges. that’s the reason for the “99.9% accuracy“. The result is but clear and, if we consider my derivation as well, which doesn’t admit approximations, then the result is exactly as it looks like.
Why would it have another meaning, or how do you know that to be the case. It states clearly that it determines π geometrically within 99.9% accuracy. That’s quite clear really, but it means that it’s just a nice way to get close, +/- 0.1%, to the TRUE value of Pi. It doesn’t disprove the traditional value of Pi.
He would be well advised to NOT make a claim that he has found a NEW and TRUE value for Pi with this construction. The number of flaws and errors identified by ChatGTP reveal the inadequacy of this document for that purpose.
*You can’t just “consider” 3.14460… to be the real π. Why would you think that?*
Of course you can, just to check up if you’re working aright. It is not a derivation of the value.
*The area that COMPLETELY covers the circle must be greater than the area of the circle itself. The area based on πr² when π=4/√φ EXCEEDS even that number so it logically cannot be the true value for Pi.*
Excedes WHAT value.? To write EXCEED you must have already a reference value and this is the mistake, you don’t have.
If you don’t know the exact value you have no reference to write „EXCEEDS“.
Based on πr^2?
You don’t have the π value!
*How did I “GUESS” something? Nowhere in the model does that happen. The numbers speak for themselves. That’s what mathematics does.*
Which numbers? If you don’t have the value you don’t have any numbers.
Let’s walk through this step by step, with specific numbers to make the results and the conclusions clear. Please read it carefully to make sure you understand each step.
The area of a circle is πr². (See the post above for an explanation of why that is, if needed.) The area of a quarter circle is π/4r²
You can see early in the YouTube video that the Desmos model results can be visually validated when the radius is 2, 5, 10 or 20. The integer number of unit squares that must be colored in to COMPLETELY cover the circle in these cases is 6, 26, 90 and 335.
We want to test BOTH possible values for π. To do so, we’ll use a radius of 2,000:
If π=3.14159… then the area of a quarter circle with a radius of 2,000 is 3,141,592.653… units squared.
If π=4/√φ (3.14446…) then the area of a quarter circle with a radius of 2,000 is 3,144,605.511… units squared.
There are NO assumptions or guessing here. We’re not CHOOSING a particular outcome. We’re CONSIDERING both! All we have done is to calculate the circle’s area as πr² for each value of Pi.
Now, what does the model tell us?
The Desmos model shows that we can COMPLETELY cover the circle by coloring in 3,143,587 full unit squares. This is a simple integer count of the colored squares.
And what does this tell us?
Since the circle is completely covered by 3,143,587 unit squares that we’ve colored in, a value for Pi that results in a lesser area of 3,141,592.653… units is a logical possibility. The actual area of the circle MUST be less than the area that COMPLETELY covers it.
The area of the circle proposed by π=4/√φ, however, EXCEEDS the complete coverage area. This 4/√φ area measure thus ALSO exceeds the area of the circle.
This proves – SIMPLY, VISIBLY AND CONCLUSIVELY – that 4/√φ CANNOT BE the true value of Pi found in a circle. The area 4/√φ predicts for a circle EXCEEDS the actual area of the circle.
That was a lengthy explanation, but this is as simple as draw a circle, color in the squares that completely cover it, count the squares and compare the count to the area measure for each value of Pi to see which one can be true. Only ONE can, and it’s 3.14159…
Note that this is the SAME value for Pi that EVERY mathematical method has derived for almost 3,000 years, and now we’ve confirmed it with a high precision digital representation of a simple physical experiment providing empirical evidence.
*Since the circle is completely covered by 3,143,587 unit squares that we’ve colored in, a value for Pi that results in a lesser area of 3,141,592.653… units is a logical possibility. The actual area of the circle MUST be less than the area that COMPLETELY covers it.*
Ok. Wait a moment.
If you already have the circle covered by 3.143’587 unit squares, then the correct value of π, according to that, should be in fact 3.143587 which is closer to 3.1446 than to 3.1415926.
No, you’ve misunderstood the model. It’s not a matter of getting closer to one value of Pi than another. It’s a question of how many unit squares completely cover the circle. If the circle is already completely covered by 3,143,587 unit squares, the area based on π=4/√φ cannot be the area of the circle. The model does not say that the correct value of Pi is 3.143587. It says that the correct value of Pi must be less than that.
*The model does not say that the correct value of Pi is 3.143587. It says that the correct value of Pi must be less than that.*
The model doesn’t say anything, it is the way you interpret it.
If the circle is already covered by 3’143’587 unit squares we can consider it the closest π value and less the 3.1415, which falls short of it.
And to that it shows that 3.1435 is closer to 3.1446 than to 3.1415, as a matter of fact.
I can’t see why we should reject it just because it is bigger. The value is closer.
The model makes the results perfectly clear.
The quarter circle can be COMPLETELY covered by 3,143,587 unit squares.
The TRUE area of the quarter CIRCLE must be LESS than the area that MORE than completely covers it.
The area of 3,144,605 based on π=4/√φ fails to meet that test, but the area of 3,141,592 based on π=3.141592… passes the test.
There is no other way to interpret this result.
Please watch the video at https://youtu.be/9Z9yfLMvAJQ to see this clearly illustrated.
*That was a lengthy explanation, but this is as simple as draw a circle, color in the squares that completely cover it, count the squares and compare the count to the area measure for each value of Pi to see which one can be true. Only ONE can, and it’s 3.14159…*
Well, this is still a guess. Just because 3.1415 is less than the „standard Circle“ you did draw doesn’t mean it is the real value. Seen this way every value below the standard circle could be considered the true value.
*Note that this is the SAME value for Pi that EVERY mathematical method has derived for almost 3,000 years,….*
Well, the methods used were not that different btw them. Basically adding the value bit by bit in endless steps. It yields always almost the same result, which is not necessarily π but the result of the method.
*…..and now we’ve confirmed it with a high precision digital representation of a simple physical experiment providing empirical evidence.*
That is interesting.
Could you give some links.
You misunderstand the model. The model doesn’t attempt to estimate the true value of Pi. It determines an area that exceeds the area of Pi, which allows us to see that the greater area value defined by π=4/√φ CANNOT be the value of Pi.
Please don’t forget to show my last comment.
The Desmos model has showed something crucial about the π value you readily overlooked.
See my responses below. I’ve not overlooked anything. You just don’t understand the model yet. Please watch the YouTube video again.
Now I get it. But this is nothing new.
2000 ys ago Archimedes set up the lower and the upper limit for the π value and yes, 3.1446 falls beyond the upper limit. But even though, 4b=π proves it to be right.
You’re getting closer to understanding, but there’s still a misunderstanding of both my model and the flaw in your own proof.
Archimedes’ goal was to approximate Pi by using polygons with more and more sides, gradually approaching the circumference of the circle from both inside and outside. This method established upper and lower bounds for Pi and has been proven accurate, supporting the value of approximately 3.14159… for nearly 2,500 years. Since then, every mathematical method, including calculus, infinite series, Monte Carlo simulations, Fourier series, fractal geometry, and continued fractions, has confirmed this value.
My model offers yet another new approach made possible by modern graphing calculators and computing power. Unlike Archimedes, who approximated the circle from within and outside, my model deliberately moves away from the circle’s circumference. The purpose is to show that π=4/√φ fails repeatedly because it overestimates the area — calculating an area larger than what is already more than sufficient to completely cover the circle.
For instance, in my model, when the radius is increased to 8,000, the circle is covered with an extra four or five unit squares beyond its circumference. Despite this, the area calculated by π=4/φ is still greater than the area that fully covers the circle. You can see this in action at this Desmos Model.
The flaw in your approach lies in assuming that 4b=π, without mathematical validation and proof that side b of your golden ratio-based Kepler triangle is actually equal to one-quarter of the circle’s circumference. In a Kepler triangle with a hypotenuse of 1 unit, side b has a length of 1/√φ. By assuming 4b=π you’re essentially claiming that 4×1/√φ=π, or 4/√φ=π, without any mathematical proof to support this assumption.
This simple step of substitution doesn’t serve as a proof. For your claim to be valid, you must mathematically demonstrate that 4b=π, rather than just making the assumption based on your inferences from the diagram you’ve created. Drawing an illustration and stating that 4b=π without any mathematical validation cannot overturn 2,500 years of solid mathematical reasoning and evidence.
Moreover, you’d also need to identify fallacies in every method that consistently confirms the traditional value of Pi. These methods all converge on the same value of π=3.14159…, further undermining the notion that π=4/√φ is correct.