As the author of this website, I’m often asked by students doing science and math projects for assistance, including answering questions when they need to interview someone on the golden ratio.
Here are some questions from Elena from Austria, who was working on her pre-scientific work as one part of her final exam to finish high school, along with my responses to her. She covered a variety of interesting topics regarding appearances and applications of the golden ratio, including phyllotaxis, identifying meaningful appearances, human attractiveness, the pyramids, art and future expectations and implications.
More importantly, she asked questions on how one can know whether a claimed appearance of the golden ratio has validity, and what significance we should find when the golden ratio is found so frequently in nature.
Occurrences of the Golden Ratio
Phyllotaxis
Pineapples: It is a well-known fact in mathematics that you can find the golden ratio and the Fibonacci-sequence on pineapples. What significance to you assign to that? (Whether mathematically or spiritually speaking)
Meisner: To understand the significance, we first need to understand the processes involved. Spirals in nature in non-biological forms (e.g., galaxies, hurricanes, waves, etc.) are generally the result of equalization of forces (e.g., gravitational, nuclear, etc.). Spirals in nature in biological forms generally produce efficiency or optimization in growth processes or use of resources, and that pattern has to be encoded in the DNA of the organism.
In the case of the alternating Fibonacci numbers that appear in plants, this pattern is the most efficient way for the plant to add additional rows, seeds or stems as it grows. The rather amazing fact about this is that these Fibonacci patterns appear only because each successive growth appears at the golden angle to the previous one. The golden angle is 137.5 degrees, which is determined by taking the 360 degrees of a circle and dividing it by 1.618… to get two sections of 222.5 degrees and 137.5 degrees.
This is illustrated in the interactive model here:
https://demonstrations.wolfram.com/PhyllotaxisSpirals/
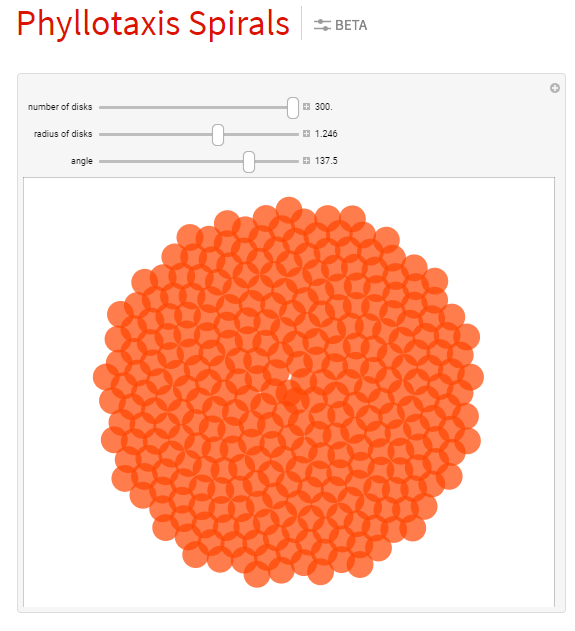
Look how different the results are when the angle is varied only slightly:
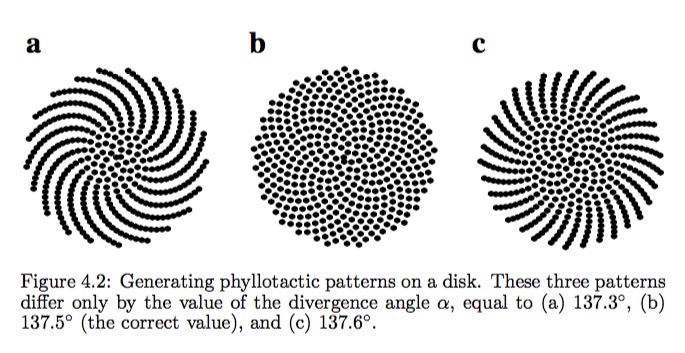
Source: http://ci47.blogspot.com/2018/04/most-rare-mathematical-proof-of-golden.html
See also an animation of the above effect at http://cmuems.com/2015c/deliverables/deliverables-09/
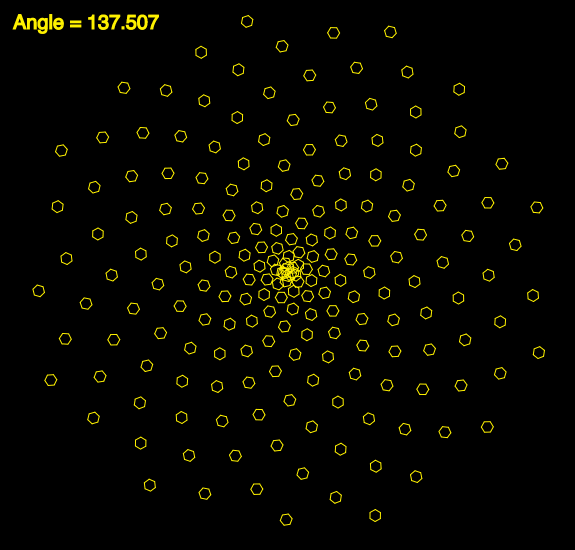
So now as to significance, we can see that plants are optimized in their patterns for growth processes and access to resources such as sunlight. We know that these patterns are encoded in their DNA. If this were achieved solely by evolution, we should expect to see that very early plants did not have this optimization. If this was achieved by design, we have to ask what was the source of the original information that was encoded in the DNA. We each need to study the evidence and come to our own conclusions about its significance.
From a spiritual perspective, the appearance in nature of mathematical optimization in biological forms gives perhaps an evidence of a greater design, and a designer. More important though is our innate ability to perceive beauty. We need to ask why we are able to perceive and experience beauty at such a deep level within our experience of life, whether that be in a face, a work of art, the spirals of a plant, the sound of music or the colors of a sunset. Is the experience of appreciating so many forms of beauty a necessary result of evolution, or was it given to us as a means to appreciate creation, and the work of our Creator? To me, that is a question we each should explore with an open heart and mind.
Meaningfulness of measures that find the golden ratio
Leaves and Branches: A lot of scientists, mathematicians and biologists have measured different leaves and branches to see if they could find the Golden Ratio. What do you think about the quote “”That there remains a certain margin in the choice of the distances to be measured and that one will seek to select the measurement in such a way that it gives the desired result.” (Source: (Beutelspacher & Petri, 1996, S. 133) quoted after. (Timerding, 1919))?
Meisner: I agree with that quote. There are a number of easily documentable appearances of the golden ratio in nature, but sometimes people set out looking for the golden ratio and find it via means that would be difficult to call statistically valid, undeniable or even convincing. This generally occurs in situations where:
- the measurement points were somewhat arbitrary, and weren’t based on the simplest or most obvious features of the object, such as it height and width,
- the results weren’t as close to the actual golden ratio as they should be to have made the claim, (e.g. 1.6 and not 1.618),
- the sample size was too small to be statistically validity or provide confidence in the conclusions,
- achieving the results required a complicated approach, or
- the observations were isolated and not part of a generally repeated pattern.
It is for all these reasons that in my work, and on page 57 of my book (The Golden Ratio – The Divine Beauty of Mathematics by Gary B. Meisner) that I apply four principles to all measures that claim to identify golden ratio proportions:
- Relevance: Appearances should be based on the subject’s most prominent or relevant features.
- Ubiquity: Appearances should appear in more than one place to demonstrate design, knowledge and/or intent rather than coincidence.
- Accuracy: Appearances should be within about 1% of the golden ratio, measured with as much accuracy as possible, and by using the highest-resolution images available.
- Simplicity: Appearances should be based on the simplest possible approaches, those that most likely would have been applied by the process, artist or designer.
When these principles are applied it drastically minimizes or eliminates the impact of a “margin in the choice of the distances to be measured,” and the “opportunity to select measurements in such a way as to give the desired result.”
Human Attractiveness
Human Beings: Which studies proof or show that the Golden Ratio on the human body seems attractive? (May you refer to some if possible)
Meisner: The relationship of the golden ratio to human facial attractiveness has been shown in studies by Dr. Stephen Marquardt, Dr. Eddy Levin, Dr. Kendra Schmid and others, including my own work. See these references:
Marquardt:
https://www.beautyanalysis.com/
https://www.discovermagazine.com/the-sciences/the-math-behind-beauty
https://www.goldennumber.net/beauty/
Levin:
http://goldenmeangauge.co.uk/about-golden-mean-gauge/
http://goldenmeangauge.co.uk/wp-content/uploads/2015/07/May2011_Arcticle.pdf
Schmid:
https://digitalcommons.unl.edu/cgi/viewcontent.cgi?&article=1098&context=csearticles
Meisner:
https://www.goldennumber.net/meisner-beauty-guide-golden-ratio-facial-analysis/
A number have studies have also been done that tried to discredit or deny the golden ratio relationship to attractiveness, but every study I’ve seen like this have been flawed in its analysis and conclusions. See my examples and analysis:
https://www.goldennumber.net/facial-beauty-new-golden-ratio/
https://www.goldennumber.net/meisner-beauty-guide-golden-ratio-facial-analysis/
https://www.goldennumber.net/golden-ratio-design-beauty-face-evidence-facts/
https://www.goldennumber.net/celebrity-faces-golden-ratio-beauty/
A Golden Universe
Golden Universe: Is it possible that we are living in a Golden Universe where the Golden Ratio is connecting everything?
Meisner: In my twenties plus years of investigation, I have found many appearances and applications in which the golden ratio does appear, but I have also found many places in which the golden ratio does not appear. Based on that, I would describe its appearance as surprisingly common and pervasive, but not universal in connecting everything.
It does though continue to found in new areas, including at the level of quantum mechanics and in cosmology, such as in black holes. Given this, it may be that we will indeed discover in the future that the golden ratio connects even more than we now know. See these links as examples. The first link in particular makes these statements:
“The golden ratio may be the fundamental constant of nature.”
“In the past the appearance of this ratio has usually been ignored by scientists because they had no way to explain it, so interest in it was considered the stuff of amateur scientists. But now, for the first time, a rigorous quantum gravity is being developed which predicts the golden ratio’s existence is literally everywhere.”
https://www.goldennumber.net/quantum-gravity-reality-golden-ratio/
https://www.goldennumber.net/quantum-matter/
https://www.goldennumber.net/quantum-time/
Uses of the Golden Ratio
The Pyramids of Egypt
Pyramids: Do you think that the ancient Egypt knew about the Golden Ratio and used it or do these significances appear just randomly? If a proof could be found what do you think would change in mathematics nowadays?
Meisner: Based on my investigations, I suspect that the ancient Egyptians had an awareness and understanding of the golden ratio, but that it was not advanced in the way we understand it now. I say this because the golden ratio is very present and observable in basic geometries and in nature, even in the simple most significant proportions of the human face. The ancients understood the relationship of a circle’s circumference to its diameter, but estimated it with integers such as 22/7. In the case of the Great Pyramid of Egypt, the base, height and hypotenuse form a golden ratio based triangle, now known as a Kepler triangle, within a precision of 0.025%:
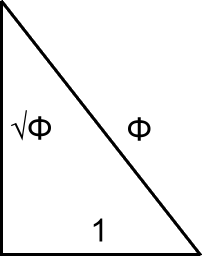
A common method at this time though to measure and construct angles for pyramids was the seked, a measure of height to width of base. It appears that the Egyptians constructed the Great Pyramid using a seked of 7 to 5.5, expressed in integers as 14 to 11. This produces a ratio of 1.272727…, which is within 0.8% of the actual golden ratio measure of 1.27202…
In my article at https://www.goldennumber.net/golden-ratio-misconceptions-by-george-markowsky-reviewed/, I show that there are only 5 right triangles based on integers from 1 to 50 that produce a variance from golden ratio dimensions of less than 1%. Of these, the triangle with a 14 to 11 ratio is the most accurate of all. So even if the Egyptians didn’t understand the golden ratio from a perspective of algebra and irrational numbers, we have to look at the evidence and ask how and why they chose a measure so very close to the golden ratio for their greatest of pyramids if it wasn’t with intent, rather than just by coincidence or accident.
The Golden Ratio in Art
Art: You pictured a few paintings from different artists and included the Golden Ratio. How do you tell if those artists included the Golden Ratio on purpose or if it was just a coincidence? Can you name artists where it is proven that they knew about the Golden Ratio and actively included it in their paintings?
Meisner: I use the same principles I listed above when analyzing the application of the golden ratio to artwork:
- Relevance: Appearances should be based on the subject’s most prominent or relevant features.
- Ubiquity: Appearances should appear in more than one place to demonstrate knowledge and intent rather than coincidence.
- Accuracy: Appearances should be within about 1% of the golden ratio, measured with as much accuracy as possible, and by using the highest-resolution images available.
- Simplicity: Appearances should be based on the simplest possible approaches, those that most likely would have been applied by the artist or designer.
You’ll notice on my image analysis that I most often use indisputable markers, such as the height and width of a canvas, or very clear and significant features of the composition. When the golden ratio is seen with pixel-level accuracy on high resolution images in the position or proportion of multiple key markers of an artist’s compositions, it becomes quite undeniable from the evidence that this could have happened by chance. Once this is established, the application by the artist of other golden ratios within a work becomes easier to establish.
Artists which I’ve found to use the golden ratio in their compositions include Leonardo da Vinci, Michelangelo, Botticelli, Raphael, Seurat, Dali and others. See the Design/Art section of my website for a variety of articles that show the evidence for this:
https://www.goldennumber.net/category/design/
See also my video on Leonardo da Vinci’s Salvator Mundi:
A key point in that video, and in most of my investigations, is that if you find compelling evidence of golden ratios using my four principles above, you may find some that weren’t intended by the artist, but can have a high degree of confidence that at least some or most of the appearances are intentional. Unless an artist explicitly documented their use of the golden ratio it can be difficult to “prove”, but as with everything from science to court cases we make reasonable assumptions based upon the available evidence and can come to solid conclusions.
Impacts of the Golden Ratio in the future
Future: What significance do you think will the Golden Ratio have in the future? In which areas will it have an important influence?
Meisner: Throughout history, the golden ratio has continued to show up in a variety of new and unexpected places. While mankind has known of it for thousands of years, just in the past 50 years it has shown up in new areas, including DNA, Penrose tiles, acoustics, quasi-crystals, quantum mechanics, black hole mathematics and more. I suspect we will continue to discover new appearances of the golden ratio, and also find new ways to apply it, in the sciences, engineering and the arts. Like most things in life, it will be limited only by our curiosity, creativity and initiative.


The Fibonacci Spiral and the Golden Ratio can describe:
planetary rotation
optimal planetary arrangement
planet distance from the Sun → link to Newton’s Law of Universal Gravitation
planet type
hypothetical planet
https://liberabaci.net/
I just finished reading your book, The Golden Ratio. In appendix A, “Further Discussion” you confront the question, “Nothing can be the Golden Ratio because it is irrational”. I’d like to present a counter-argument to that question, that the Golden Ratio is special because it is the most irrational number.
Specifically, the reason that nature chose the Golden Angle for the phyllotaxis, is that it is the most irrational number turn of a circle that solves the engineering problem of distributing points around a circle in such a way that seeds, leaves or petals are less likely to interfere with each other.
Obviously, a rational number cannot be used for this purpose because it would create ‘spokes’ at each partial turn that corresponds to the common divisor of the angle chosen, for example, 1/3 or 2/3 of a turn would create three spokes at 0, 120°, 240°.
Other irrational numbers are usually not suited, because in general, they usually have pronounced spokes at places early in the sequence, that eventually slowly spiral around the circle.. (This can be verified with the Wolfram applet linked in the blog post)
The Golden Angle wins out over other irrational numbers, In that it produces the most even distribution with low numbers of iterations of the phyllotaxis process. I’m not sure how to succinctly prove this mathematically, but consider the continued fraction representation of the Golden Ratio: 1+(1/(1+1/(1+1/…))) which implies a uniform smoothness to its irrationality..
This can also be used to explain why we see Fibonacci and Lucas Numbers in the count of spirals originating from the origin point of a phyllotaxis process, because the ratio of adjacent members of these sequences rapidly converge to the Golden Ratio, these spirals serve as the ‘spokes’ that approximate it.
All good points about the uniqueness of the golden ratio that makes it suitable for phyllotaxis.
I think though that you misunderstood the point of the discussion on the statement, “Nothing can be the Golden Ratio because it is irrational.” There are certain writers on the golden ratio who try to say that NOTHING in the material world can “be” the golden ratio for the simple reason that the golden ratio has an infinite number of digits and nothing in the material world could be that accurate. So by their logic, the golden ratio cannot appear in phyllotaxis because any angle that one claimed to be a golden angle would be off by some small amount and thus not really be a golden angle.
To me this is a rather pointless argument. As you noted, the golden ratio and golden angle DO appear in phyllotaxis. The small differences make no difference in the application or in our understanding of the principles involved. By their logic, we might as well say that we can’t have circular wheels because the circle will never perfectly accurate. We can’t even drill a 1″ hole because that too will not be perfectly 1″. It’s just the nature of the material world, and has no meaningful impact on our application of the concepts.
Take any rational approximation of Phi, for instance 13/8 and you know that 8/13 + 1 is not 13/8 again but 21/13