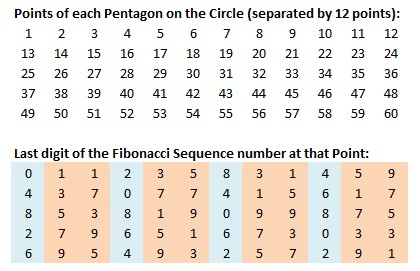
The last digit of the numbers in the Fibonacci Sequence form a pattern that repeats after every 60th number:
0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1
This pattern can be seen in the following list of the first 72 Fibonacci numbers:
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1,597 |
| 18 | 2,584 |
| 19 | 4,181 |
| 20 | 6,765 |
| 21 | 10,946 |
| 22 | 17,711 |
| 23 | 28,657 |
| 24 | 46,368 |
| 25 | 75,025 |
| 26 | 121,393 |
| 27 | 196,418 |
| 28 | 317,811 |
| 29 | 514,229 |
| 30 | 832,040 |
| 31 | 1,346,269 |
| 32 | 2,178,309 |
| 33 | 3,524,578 |
| 34 | 5,702,887 |
| 35 | 9,227,465 |
| 36 | 14,930,352 |
| 37 | 24,157,817 |
| 38 | 39,088,169 |
| 39 | 63,245,986 |
| 40 | 102,334,155 |
| 41 | 165,580,141 |
| 42 | 267,914,296 |
| 43 | 433,494,437 |
| 44 | 701,408,733 |
| 45 | 1,134,903,170 |
| 46 | 1,836,311,903 |
| 47 | 2,971,215,073 |
| 48 | 4,807,526,976 |
| 49 | 7,778,742,049 |
| 50 | 12,586,269,025 |
| 51 | 20,365,011,074 |
| 52 | 32,951,280,099 |
| 53 | 53,316,291,173 |
| 54 | 86,267,571,272 |
| 55 | 139,583,862,445 |
| 56 | 225,851,433,717 |
| 57 | 365,435,296,162 |
| 58 | 591,286,729,879 |
| 59 | 956,722,026,041 |
| 60 | 1,548,008,755,920 |
| 61 | 2,504,730,781,961 |
| 62 | 4,052,739,537,881 |
| 63 | 6,557,470,319,842 |
| 64 | 10,610,209,857,723 |
| 65 | 17,167,680,177,565 |
| 66 | 27,777,890,035,288 |
| 67 | 44,945,570,212,853 |
| 68 | 72,723,460,248,141 |
| 69 | 117,669,030,460,994 |
| 70 | 190,392,490,709,135 |
| 71 | 308,061,521,170,129 |
| 72 | 498,454,011,879,264 |
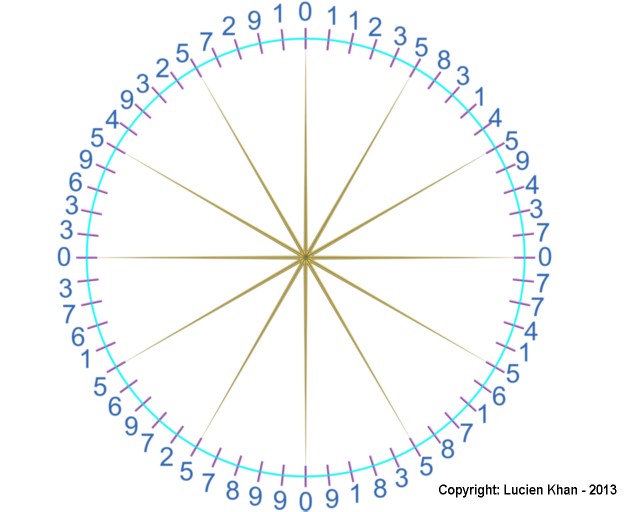
Lucien Khan arranged these 60 digits of the pattern in a circle, as shown in illustration below:
Here he found other interesting results:
- The zeros align with the 4 cardinal points on a compass.
- The fives align with the 8 other points of the 12 points on a clock.
- Except for the zeros, the number directly opposite each number adds to 10.
Lucien postulates that ancient knowledge of these relationships contributed to the development of our modern use of 60 minutes in an hour, and presentation of numbers on the face of the clock.
I found too that any group of four numbers that are 90 degrees from each other (15 away from each other in the circle) sum to 20, except again for the zeros. As an example, use 1, 7, 9 and 3, which appear one to the right of each of the compass points.
Additionally, every group of five numbers that define the points of the 12 pentagons on the circle also create a pattern. Four of the pentagons have even-numbered last digits of 0, 2, 4, 6, and 8. The remaining eight pentagons have odd-numbered last digits of 1, 3, 5, 7 and 9.
Another interesting pattern yet was observed by Lucien Khan: The 216th number is this sequence is 619220451666590135228675387863297874269396512. The sum of all the digits in that number add up to 216, as well. He notes that it is believed that the secret or hidden name of God contains 216 characters. There are many other fascinating relationships and sacred geometries, which are presented by Lucien Khan in more detail at the links below.
References:
https://docs.google.com/document/d/1mVWd1aLiYZQU8VvYFBnW8kxodeYim3bYDIFfh-w42eU/pub
https://www.youtube.com/watch?v=bY5zwXXoUHc



The compass thing is very impressive but I think finding the name of God is going a bit too far!
Maybe, but if you do a Google search for “name of god 216 letters” you’ll find 1.6 million references. See https://www.google.com/search?q=name+of+god+216+letters
“Maybe, but if you do a Google search for “name of god 216 letters” you’ll find 1.6 million references. ”
Only 1.6 mio? Well if it were really true it would have been 216 million. So, checkmate!
Not so fast there. First, your assumption that the two number should agree is not all that logical. Google is just a man made search engine, not a divine revelation of scripture or nature. Second, a checkmate is a check from which the king cannot escape. Just since my post, the number of Google references has increased to 2.1 million references. That means that human awareness is growing, but will never fully comprehend God. So, checkmate!
Duly noted sir!
I’ve actually found the tetragrammaton inside this sequence. I’ve created this design and animation:
See the explanation: https://rgkevin.github.io/golden-clock/
Could you explain your Golden clock further, the link wasn’t working…
This makes an interesting connection with the dodecahedron which has 12 faces of 5 sides each. I wonder what would happen if we expressed the Fibonacci in sexuagesimal, base 60 notation as used by the Sumerians.
The use by the Sumerians of base 60 for their number scheme is added evidence that the number 60 had special significance to the ancients.
Just for the record, I wrote about this wheel of 60 in a published book in 2010, 3 years before Khan, showing the 60 Pattern and the cardinal alignment of the zeroes. It is in one of my 9 books from the series THE BOOK OF PHI, volume 3, sub-titled “The 108 Codes, an Introduction” pages 35 onwards, chapter 3, called Time Code 12:24:60 Encrypted in the Fibonacci Sequence.
To review or buy this book, click on the link
http://www.jainmathemagics.com/bookofphivol3/
and an ebook version is also available
http://www.jainmathemagics.com/ebookofphivol3/
Regards, Jain 108
I was surprised by the 216th fibonacci number find. Number of compound letters in the Tamil alphabet is 216. Interesting coincident isn’t it?
I would guess this fact is probably the very reason why 216 is related to God’s name.
Since Tamil is the oldest culture and original language of the world, it makes sense that later cultures based on Tamil retains information of that great divine concept of alphabet but covered with the mist creating the mystery of secret God’s name consisting of 216 letters.
Btw, I am not Tamil. I am not saying that Tamil is oldest to promote myself. I am saying it because it is most probably the truth and it is unfortunately widely ignored, what in turn leads to mist and mystery instead of clear logical explanations.
Older cultures didn’t have an alphabet, but correct me if I’m wrong. I am not sure what cultivation means, but I cannot imagin it started with an alphabet, let alone a number considdered to be a name.
In the example where the 60 numbers are arranged to define the five points of the twelve pentagons (five rows of twelve numbers). i found that by arranging the numbers in 12 rows of 5 numbers, 10 rows of 6 numbers, 6 rows of 10 numbers all produced the same interesting related patterns within each column. I began each arrangement starting with 1, as in the start of the sequence. ex. 1, 1, 2, 3, 5 etc. This subject of the Golden Ratio and the Fibonacci sequence and how it relates to God fascinates me and finding this information presented here has piqued my curiosity like never before. i’m hooked.
Do you have the visual presentation of your idea, or web site where we can read more about it.
Thanks!
In this compas, right next to zeros there are always numbers 1,3,5,7 (typical endings of prime numbers) – this little detail can be a connection beetwen Fibonnaci numbers and Primes.
And if you check Lucas numbers you find a pattern of 12 digits that have an intersting connection to this compas too.
I don’t know why it repeats with the power of 7 (1,7,9,3) one way and 3 (3,9,7,1) the other way, but the fact that those 2 mirror each other is rather far from a miracle.
Can be reduced to 20 numbers by doubling the sequence: 02246066280886404482
Fragment of a 3 x 20 matrix:
0 1 1 2 3 5 8
1 6 7 3 0 3 3
1 7 8 5 3 8 1
2 3 5 8 3 1 4
3 0 3 3 6 9 5
5 3 8 1 9 0 9
8 3 1 4 5 9 4
3 6 9 5 4 9 3
1 9 0 9 9 8 7
4 5 9 4 3 7 0
Like this ?
11235
83145
94370
77415
61785
38190
99875
27965
16730
33695
49325
72910
Technically, the 0 you have in 72910 at the end should have been the first digit in 01123, which changes each of the 12 groups of 5 numbers you listed.
0 1 1 2 3
5 8 3 1 4
5 9 4 3 7
0 7 7 4 1
5 6 1 7 8
5 3 8 1 9
0 9 9 8 7
5 2 7 9 6
5 1 6 7 3
0 3 3 6 9
5 4 9 3 2
5 7 2 9 1
(thank you for the correction)
The Lucas-number equivalent:
2 1 3 4 7
1 8 9 7 6
3 9 2 1 3
4 7 1 8 9
7 6 3 9 2
1 3 4 7 1
8 9 7 6 3
9 2 1 3 4
7 1 8 9 7
6 3 9 2 1
3 4 7 1 8
9 7 6 3 9
No zeros or fives
Better to write it like this:
055055055055
189
13
21
34
55
89
(the initial comment was meant as a reply to Wojtek February 2, 2018 at 8:06 am)
Another nice line up:
1. 0 1. 1. 2. 3. 5. 8.
3. 1. 4. 5. 9. 4. 3
7. 0. 7. 7. 4. 1. 5. 6
1 7. 8. 5. 3. 8. 1
9. 0. 9. 9. 8. 7. 5. 2
7. 9. 6. 5. 1. 6. 7
3. 0. 3. 3. 6. 9 5. 4
9. 3. 2. 5. 7. 2. 9.
1 0. 1. 1. 2. 3. 5. 8
3. 1 ….
7 0. ..
1….
That didn’t come across too well; it should have looked something like this:
1-0-1-1-2-3-5-8
-3-1-4-5-9-4-3
7-0-7-7-4-1-5-6
-1-7-8-5-3-8-1
etc.
Which can be read bottom/up (diagonally) as:
1-0-1-1-2-3-5-8
-7-0-7-7-4-1-5-6
1-9-0-9-9-8-7-5-2
-7-3-0-3-3-6-9-5-4
If you take every fifth number it produces the last digit cycle of the Lucas numbers. with exception of the zeros and fives.
213471897639
First digit is a zero so all we have is 055055055055
Next digit is 1897639 21347 Then it repeats 1897639 21347
Next digit is 13471897639 2 Then it repeats 13471897639 2
Next digit is 213471897639 Then it repeats 213471897639
Next digit is 3471897639 21 Then it repeats 3471897639 21
Astonishing the Lucas sequence is that present in the last digits of the Fibinacci sequence (apart from the binary string.)
In general it is quite strange both the decimal and the hexidecimal system suit the Fibonacci numbers that well, but maybe it’s the other way around which makes it even more mysterious.
If you order the last digits of the Fibonacci-numbers in 5 rows of 12 as in the table above::
011235831459
437077415617
853819099875
279651673033
695493257291
each row can be turned into the same sequence of last Lucas numbers digIts by adding every second number (even and uneven n)
1347189763
1347189763
1347189763
1347189763
1347189763
And if you take the natural numbers and multiply them by 4, the last digits are the first column
The last digits of squared fibonacci numbers add up after a period of 15 numbers::
0, 1, 1, 4, 9, 25, 64, 169, 441, 1156, 3025, 7921, 20736, 54289, 142129, 372100,
974169, 2550409, 6677056, 17480761, 45765225, 119814916, 313679521, 821223649, 2149991424
The same accounts for golden rectangles::
0, 1, 2, 6, 15, 40, 104, 273, 714, 1870, 4895, 12816, 33552, 87841, 229970,
602070, 1576239, 4126648, 10803704,, 28284465, 74049690, 193864606, 507544127, 1328767776, 3478759200, 9107509825, 23843770274
I’ve long known these series, but I’ll give you another,,not just the last digit but each number reduced to a single digit repeats itself after 24 times. So you got the minutes and here are the hours 😉
112358437189887641562819 then it starts again 1123584 etc. The reason and why it does so is to lengthily to explain here, but I can say this, there is structure behind numbers.
This has long been known to me, you have the minutes so I will give the hours 24, and will repeat itself
Again take the whole numbers and reduce to single digit like 46368 is 4+6+3+6+8=27 2+7=9.
It would ne to much to write it all down hère but thé reason ans how van ne explained as thé is a structure upon which thèse numbers are placed..,this has far reaching consequences when shown so it can not be done
As a reply.
All 60 numbers from a different perspective:
0 2 6 6 2 0 8 4 4 8 (0)
5 9 7 7 9 5 1 3 3 1 (5)
5 3 9 9 3 5 7 1 1 7 (5)
0 6 8 8 6 0 4 2 2 4 (0)
5 7 1 1 7 5 3 9 9 3 (5)
5 9 7 7 9 5 1 3 3 1 (5)
Extended:
0 2 6 6 2 0 8 4 4 8 0 2 6 6 2 0
5 9 7 7 9 5 1 3 3 1 5 9 7 7 9 5
5 3 9 9 3 5 7 1 1 7 5 3 9 9 3 5
0 6 8 8 6 0 4 2 2 4 0 6 8 8 6 0
5 7 1 1 7 5 3 9 9 3 5 7 1 1 7 5
5 9 7 7 9 5 1 3 3 1 5 9 7 7 9 5
0 8 4 4 8 0 2 6 6 2 0 8 4 4 8 0
5 1 3 3 1 5 9 7 7 9 5 1 3 3 1 5
5 7 1 1 7 5 3 9 9 3 5 7 1 1 7 5
0 4 2 2 4 0 6 8 8 6 0 4 2 2 4 0
5 3 9 9 3 5 7 1 1 7 5 3 9 9 3 5
5 1 3 3 1 5 9 7 7 9 5 1 3 3 1 5
0 2 6 6 2 0 8 4 4 8 0 2 6 6 2 0
5 9 7 7 9 5 1 3 3 1 5 9 7 7 9 5
5 3 9 9 3 5 7 1 1 7 5 3 9 9 3 5
0 6 8 8 6 0 4 2 2 4 0 6 8 8 6 0
5 7 1 1 7 5 3 9 9 3 5 7 1 1 7 5
5 9 7 7 9 5 1 3 3 1 5 9 7 7 9 5
Arguably the most symmetrical representation of the last digits
0 3 9 4 3 5 2 1 1 2 5 3 4 9 3 0
0 1 3 8 1 5 4 7 7 4 5 1 8 3 1 0
0 7 1 6 7 5 8 9 9 8 5 7 6 1 7 0
0 9 7 2 9 5 6 3 3 6 5 9 2 7 9 0
This way it can be closed like a book with all 6o (55) digits adding up to 10 as in the circle
3 6 5 9 2 7 9 0 1 3 8 1 5 4 7
1 2 5 3 4 9 3 0 7 1 6 7 5 8 9
7 4 5 1 8 3 1 0 9 7 2 9 5 6 3
9 8 5 7 6 1 7 0 3 9 4 3 5 2 1
It can be viewed a product of these 2
3 8 5 3 2 1 1 0 1 1 2 3 5 8 3
3 8 5 3 2 1 1 0 1 1 2 3 5 8 3
3 8 5 3 2 1 1 0 1 1 2 3 5 8 3
3 8 5 3 2 1 1 0 1 1 2 3 5 8 3
1 7 9 3 1 7 9 0 1 3 9 7 1 3 9
7 9 3 1 7 9 3 0 7 1 3 9 7 1 3
9 3 1 7 9 3 1 0 9 7 1 3 9 7 1
3 1 7 9 3 1 7 0 3 9 4 1 3 9 7
This seems to be the underlying pattern (matrix) responsible for the repetition.
5 5 0 5 5 0 5 5 0 5 5
5 0 5 5 0 5 5 0 5 5 0
0 5 5 0 5 5 0 5 5 0 5
Since it also works with the natural numbers, it might have little to do with the Fibonacci-sequence and more with the decimal system.
0 1 2 3 4 5 6 7 8 9
5 6 2 8 9 5 1 2 8 4
0 6 7 3 9 0 6 2 3 9
0 1 2 3 4 5 6 7 8 9
(adding the binary matrix to the natural numbers)
Similar to the Liber Abaci-numbers
0 1 1 2 3 5 8 3 1 4 5
5 1 6 7 3 0 3 3 6 9 5
5 6 1 7 8 5 3 8 1 9 0
0 1 1 2 3 5 8 3 1 4 5
In chronological order:
0 1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1
5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6
5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1
0 1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1
As the ‘clock’ turns with the power of three, so does each string when 5’s are subtracted.
0 1 1 2 3 0 3 3 6 9 0 9 9 8 7 0 7 7 4 1
This follows from a 3/5 sequence: 3,5,35,355,33555,33355555,3333355555555,
As every 5th is a 5-fold, another 055055-string is added:
0
1
1
2
3 0
0 5
3 5
3 0
6 5
9 5 0
0 0 5
9 5 5
9 5 0
8 0 5
7 5 5 0
0 5 0 5
7 0 5 5
7 5 5 0
4 5 0 5
1 0 5 5 0
0 5 5 0 5
.
I have made some new discoveries on the Fibonacci 60 Code, refer to my website:
https://www.jain108.com/fiboncci-60-code/
JAIN’S DISCOVERY: Fibonacci 60 Code: Spiral Pattern of ReEntry
I am proud to release another rare gem based on the Infinitely Repeating 60 Final Digits of the Fibonacci Sequence. When I plotted the 60 numbers on graph paper, (like the work of Ulam’s Rose revealing the 24 Pattern of Prime Numbers, and the stock-marketeering work of Gann’s Wheel of 24) I discovered that after 60 steps, the pattern RE-ENTERS ITSELF or ends where it begins, thus forming a predictive, cyclic pattern of the highest order that has applications with 60 hertz frequency and other hi-tech connections regarding frequency and vibration. It asks the question, did Tesla base his life-giving innovations on this distinctive 60 periodicity that obeys the Laws of Nature.
Jain 108
ps: I will explain this in further detail on Facebook soon. This revelation has never been published before in print and will appear as a 15 minute video discourse.
Hello Jain. Your page above at https://www.jain108.com/fiboncci-60-code/ is a real treasure of Fibonacci relationships, both mathematically and visually. Thanks much for your very creative and revealing work on this, Jain, and for sharing it with readers here. Regards, Gary Meisner
Quite obvious, but yet not noted is the fact that one can read the circle counterclockwise as:
0, 1, -1, 2, -3, 5, -8 using subtraction instead of addition.
There is another nice pattern based on Fibonacci squares.
The 72nd and last Fibonacci number in the list ends with the square of the sixth Fibonacci number (8) which is 64
72 = 2 x 6^2
Almost magically the 50th Fibonacci number ends with the square of the fifth Fibonacci number (5) because 50/2 is the square of 5.
So the square of the 4th Fibonacci number might correspond with the last digit(s) of the 2 x 4^2 = 2 x 16 = 32nd Fibonacci number; and yes it does. Here’s a little video showing (off) this relationship by forming a spiralling square of all the 60 last digits: https://youtu.be/-9IjAFBvPzg
Checking the end digits of the golden squares:
0, 1, 1, 4, 9, 5, 4, 9, 1, 6, 5, 1, 6, 9, 9, 0
0, 9, 9, 6, 1, 5, 6, 1, 9, 4, 5, 9, 4, 1, 1, 0
the repeating period is 30 digits long and has a cross-over decimal symmetry. that can be split in half once more revealing a familiar pattern.
0, 1, 1, 4, 9, 5,
5, 4, 9, 1, 6, 5,,
5, 1, 6, 9, 9, 0,
0, 9, 9, 6, 1, 5
5, 6, 1, 9, 4, 5,
5, 9, 4, 1, 1, 0,
Each half can be split in 3 I meant, The last digit sequence of squared Lucas numbers 419691 has been encountered before in a 6 x 10 table of the Fibonacci last digit sequence:
011235831, 4
594370774, 1
561785381., 9
099875279, 6
516730336, 9
549325729, 1
(011235831, 4)
The nature of the relationship n –> 2n^2 is still a mystery to me; anyone ?
Here’s a nice little arithmetic curiosity: 1/89=0.112358… (as known).
(But) 55/89 = 0,6179775280898876…which differs only in that it starts with the 21st last digit (times 10) and the 22nd. Moreover the inverse (89/55) is: 1,618181818181818
Yes, see more on 1/89 at https://www.goldennumber.net/89-and-109/.
216 letters or 6x6x6 letters…
For it is the number of a man; and his number is 6 6 6
The Fib-square final digit numbers in order
2 1
8 21
18 2,584
32 2,178,309
50 12,586,269,025
72 498,454,011,879,264
2n²
If u use 2 at the begining instead of a 1 example 022460662 ect … It repeats 20 times if u use 5 055055055 only 3 times https://youtu.be/30T-NDTjPRI here is a video i made
I like that circle, always after O we can see a double odd numbers 11, 77, 99, 33.
Dear All,
I’m sorry this is a very long message.
I was delighted & very excited to find your website, Golden Number.net, today after trying for several hours to work out how a particular “Fibonacci design” works (I was originally searching for inspiration for a painting)! I worked out part of it myself, but then was completely lost! I knew that the last digits of the numbers in the Fibonacci sequence have a repeating pattern of 60, but I just didn’t know what was going on with the rest of this particular design.
I wish I was as mathematically brilliant as you all are! I got lost quickly (again) when I saw all your posts about the different matrices! But the things I understood amazed me & just reminded me again that mathematics is a language of God, that shows the truth of God & couldn’t exist without Him!
So I have a few questions that I would be very grateful if anyone can answer, if you have time: I’m sorry my questions are not phrased in very mathematical terms! I first became fascinated by Fibonacci patterns in nature when I was studying on an Agricultural Botany Bsc degree course, specifically when we were learning about apical meristems & patterns of plant growth.
I would like to paint a similar design, maybe utilising the Fibonacci scale as related to colours. But I know there are twice as many Fibonacci sequence numbers ending in an odd number as there are those ending in an even number, so I would want to put the colours I most prefer in the positions of the odd numbers & my less preferred colours in the positions of the even numbers. I want to understand as fully as possible the basis for any design I end up drawing/painting. I think using colours makes it a bit easier to see mathematical patterns, for me anyway. Also, I would make the widths of the different circles in Fibonacci sequence proportions.
Also, I felt a bit strange reading the comments about 0 & 5, because my birthday is 05/05 in our current calendar!
This is the link to the design I’m asking about: https://www.deviantart.com/wibblebubble/art/infinite-circular-fibonacci-pattern-579062601
So, my questions/comments are as follows:
If:
0 = Outer circle = 6 x sequence of 10 colours = total 60 segments
1 = Next innermost circle of 60 segments = Fibonacci sequence in clockwise direction, taking just the last digit of each Fibonacci number to determine the colour used
then working inwards to get to higher circle numbers, all with 60 segments
2 = Next innermost circle = Fibonacci sequence in anticlockwise direction, taking just the last digit of each Fibonacci number to determine the colour used
Question/Comment: Is that related to the comment by “D Says” about the circle being able to be read counterclockwise by subtraction, instead of clockwise by addition? I understand that the last digits of the Fibonacci Sequence have a repeating cycle of 60 digits, so I guessed that was why the artist reversed the direction in Circle 2, or it would have had exactly the same colours in each segment as Circle 1, although some of the segments do have the same number/colour in the clockwise & the anti-clockwise circles.
3 = the circle where it started to get very complicated for me! I had a few ideas about how it was working, which worked some of the time but not all the time, so I knew those ideas of mine were not the correct answer!
Question/Comment: This seems to be related to peoples’ comments about 0 & 5, if I’ve understood correctly, if not, can someone please explain?
4 = the circle where my brain just collapsed & I lost it totally, even though I tried to understand it and relate it to peoples’ comments! Plus there are no odd-ending numbers in that circle, just 0 & even-ending numbers.
Question/Comment: I think the artist did it that way for a particular reason, please can anyone explain it to me in a simple way?
Also, would there be a 5th or further circles inwards, building further on the previous ones or other Fibonacci number theory?
What would be in the centre, if anything other than zero?! And why?! Or it is really infinite, as the title of the design suggests? Obviously there is no way to draw infinity in the centre, unless leaving it blank is the answer!
It seems the artist who created this knew a lot more than is obvious on first seeing this design & deliberately did everything in a particular way, with nothing random about it at all. At first I wondered why the outer circle “0” was there, but then saw that it can be used to count the spacing of the numbers/colours in the inner circles.
Unfortunately, there is no description by the artist as to the basis of this design, or even their name, unless I missed those details.
I hope someone has the time to answer my questions, but, if not, I understand people are busy & I thank you all for being so inspiring anyway.
Kind regards,
Rhona Bloxsom.
First double the remainders in base 10:
0224606628
0886404482
then half them:
01123
03314
04432
02241
01123
2ⁿmod(5): 1,2,4,3,1
3ⁿmod(5): 1,3,4,2,1
Lucas numbers mod(5): 2,1,3,4,2,.