Fibonacci Series and Golden Section - General Links Dr. Ron Knott's Fibonacci Numbers and the Golden section Site - One of the most thorough sites on the Internet on this topic, and a winner of many awards. The Museum of Harmony and Golden Section Fibonacci Quarterly Home Page - Research Magazine The life and numbers of Leonardo Fibonacci Fascinating Fibonaccis - … [Read more...]
Golden Ratio Software
PhiMatrix - PhiMatrix is a graphic analysis and design tool that lets you see and apply phi proportions to any image. PhiMatrix software unveils the phi proportions that can be found in DNA, sea shells, plants, animals and human faces and even in the stock market. It features a grid that can be locked to golden section proportions or unlocked to vary height and width while … [Read more...]
Books, etc.
Elliott Wave International For those interested in applying Fibonacci numbers to stock market analysis, Elliott Wave International (EWI) is one of the world's largest providers of market research and technical analysis. Their staff of full-time analysts provides global market analysis via electronic online services to institutional investors 24 hours a day. EWI also provides … [Read more...]
The Golden Section / Golden Ratio
GoldenNumber.Net explores the appearance of Phi, 1.618 (also known as the Golden Ratio, Golden Mean, Golden Section or Divine Proportion, in mathematics, geometry, life and the universe and shows you how to apply it, and its applications are limitless: Art Architecture Design of any kind – Graphics, logos, products, fashion, web sites and more Photo composition, photo … [Read more...]
Powers of Phi
Phi has a unique additive relationship. The powers of phi have unusual properties in that they are related not only exponentially, but are additive as well. We know that: Phi 2 = Phi + 1 Which is the same as: Phi 2 = Phi 1 + Phi 0 And this leads to the fact that for any n: Phi n+2 = Phi n+1 + Phi n Thus each two successive powers of phi add to the next … [Read more...]
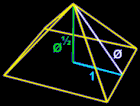
Pi, Phi and Fibonacci
Phi (Φ) and pi (Π) and Fibonacci numbers can be related in several ways: The Pi-Phi Product and its derivation through limits The product of phi and pi, 1.618033988... X 3.141592654..., or 5.083203692, is found in golden geometries: Golden Circle Golden Ellipse Circumference = p * Φ Area = p * Φ Ed Oberg and Jay A. Johnson have developed a unique expression … [Read more...]
The Phi Formula
Is the formula for Phi unique or should we say, "Hey, it's just an expression!" It's been noted by some who say they can "demystify phi" that phi is just one of an infinite series of numbers that can be constructed from the following expression using the square root (√) of integer numbers: (1+√n) / 2 It just so happens that you get phi when you let n equal 5. Let n be other … [Read more...]
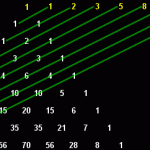
Pascal’s Triangle
The Fibonacci Series is found in Pascal's Triangle. Pascal's Triangle, developed by the French Mathematician Blaise Pascal, is formed by starting with an apex of 1. Every number below in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero. The numbers on diagonals of the triangle add … [Read more...]
Fibonacci 24 Repeating Pattern
The Fibonacci sequence has a pattern that repeats every 24 numbers. Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4. Applying numeric reduction to the Fibonacci series produces an infinite series of 24 … [Read more...]
89, 109 and the Fibonacci Sequence
The reciprocal of 89, a Fibonacci number, is based on the Fibonacci series. This is a little curiousity involving the number 89, one of the Fibonacci series numbers. 1/89 is a repeating decimal fraction with 44 characters: .01123595505617977528089887640449438202247191 You can see the beginning of the Fibonacci sequence in the first 6 digits of the decimal equivalent of … [Read more...]