Creating a Triangle based on Phi (or Pythagoras meets Fibonacci):
Pythagoras discovered that a right triangle with sides of length a and b and a hypotenuse of length c has the following relationship:
a² + b² = c²
A foundational equality of phi has a similar structure:
1 + Phi = Phi2
( 1+ 1.618… = 2.618… )
By taking the square root of each term in this equality, we have the dimensions of a triangle, known as a Kepler Triangle, a right triangle based on this phi equality, where:
| Side | Length squared per above | Length, or square root | Length divided by phi so c = 1 |
| a | 1 | 1 | 1 / Phi |
| b | Phi | √ Phi | 1 / √ Phi |
| c | Phi2 | Phi | 1 |
This triangle is illustrated below. It has an angle of 51.83° (or 51°50′), which has a cosine of 0.618 or phi.
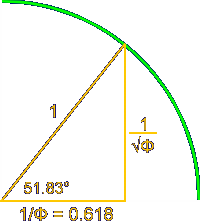
The Pythagorean 3-4-5 triangle is the only right-angle triangle whose sides are in an arithmetic progression. 3 + 1 = 4, and 4 plus 1 = 5. The Kepler triangle is the only right-angle triangle whose side are in a geometric progression: The square root of phi times Φ = 1 and 1 times Φ = Φ.
Although difficult to prove with certainty due to deterioration through the ages, this angle is believed by some to have been used by the ancient Egyptians in the construction of the Great Pyramid of Cheops.
Other triangles with Golden Ratio proportions can be created with a Phi (1.618 0339 …) to 1 relationship of the base and sides of triangles:
The isosceles triangle above on the right with a base of 1 two equal sides of Phi is known as a Golden Triangle. These familiar triangles are found embodied in pentagrams and Penrose tiles.
|
|
|
Creating a Triangle based on Fibonacci numbers
No three successive numbers in the Fibonacci series can be used to create a right triangle. Marty Stange, however, contributed the following relationship in January 2007: Every successive series of four Fibonacci numbers can be used to create a right triangle, with the base and hypotenuse being determined by the second and third numbers, and the other side being the square root of the product of the first and fourth numbers. The table below shows how this relationship works:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
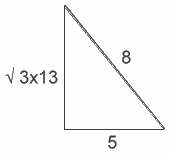
Thus for the illustration highlighted in gold, Stange’s Treatise on Fibonacci Triangles reveals that a triangle with sides of 5 and the square root of 39 (e.g., 3 x 13) will produce a right triangle with a hypotenuse of 8.
As greater numbers in the series are used, the triangle approaches the proportions of the phi-based Kepler Triangle above, with a ratio of the hypotenuse to the base of Phi, or 1.618…
What a brilliant analysis by Stange. I loved your beautifully done illustrations, and how clear your descriptions were.
Anyone interested in phi should look up how using the Fibonacci numbers can create a series of rectangles that approach the phi ratio.
A very useful presentation and quite interesting!
CORRECT REPETITION
————————
A very interesting topic.
My decoding Plato’s Timaeus “MOST BEAUTIFUL TRIANGLE” shows that Kepler / Magirus Triangle is a similar triangle, “not the same” and” not as beautiful” , but constituent to that of Plato’s:
http://www.stefanides.gr/Html/quadrature.htm
This orthogonal scalene triangle has all its sides in ratio T and scalene angle ArcTan [ T ] , T=SQRT[Phi].
Its hypotenuse is T^3, its bigger side is T^2 and its smaller is T^1.
{ http://www.stefanides.gr/Html/gmr.htm
Shows the ruller and compass structure of T [ = sqrt(Phi) ] and Θ [ = ArcTan(T) ] ,
via known construction of Phi [ = T^2].
It is based on a fourth order equation : T^4 – T^2 -1 =0 }
For quadrature of circle, [ as proved imposibility by transcendentals ] is obtained , however, by the irrational value of 4/[SQRT(Phi)] , following the equation : [ Πσχ ]^4 + { [ Πσχ ]^2}*4^2 – 4^4 =0
Ref: http://www.stefanides.gr/Html/piquad.htm
And an AutoCad drawing:
http://www.stefanides.gr/pdf/D=5,083FOUR_1.pdf
© Copyright 1999 P. C. Stefanides.
Regards,
Panagiotis Stefanides
REF:
http://www.stefanides.gr/pdf/BOOK_1997.pdf
GEOMETRIC CONCEPTS IN PLATO
Panagiotis Stefanides
http://www.stefanides.gr
Awesome explanation. Thank you!!
Really started loving golden ratio
One more amazing Golden Triangle exists, although unknown long time.
It is described and represented here:
http://eye-of-revelation.org/PDF/THEORY-SriYantra.pdf
© 2003 The Watch Publisher
Completed further descriptions of the Great Golden Triangle,
as well as the Golden Section-s in the Vitruvian Man by Leonardo da Vinci updated here:
https://golden-ratio.eye-of-revelation.org/
© 2019 The Watch Publisher
Because the powers of Phi, unlike other numbers, are in Phi ratio to one another AND are in an additive sequence where any member is the sum of the prior two, it naturally follows that
Right triangle sides a,b,c where c is hypontenuse. IF a = phi^n and c= phi^(n+1)
THEN b must equal phi^ ((n+2)/2)
Beautiful work. A real joy. Thank You.