Penrose Tiling and Phi

Tiling in 5-fold symmetry was thought impossible!

Areas can be filled completely and symmetrically with tiles of 3, 4 and 6 sides, but it was long believed that it was impossible to fill an area with 5-fold symmetry, as shown below:

The solution was found in Phi, the Golden Ratio

In the early 1970’s, however, Roger Penrose discovered that a surface can be completely tiled in an asymmetrical, non-repeating manner in five-fold symmetry with just two shapes based on phi, now known as “Penrose tiles.”

This is accomplished by creating a set of two symmetrical tiles, each of which is the combination of the two triangles found in the geometry of the pentagon.

Phi plays a pivotal role in these constructions.  The relationship of the sides of the pentagon, and also the tiles, is Phi, 1 and 1/Phi.

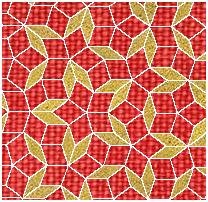
The triangle shapes found within a pentagon are combined in pairs.	One creates a set of tiles, called “kites” and “darts” like this:	The other creates a set of diamond tiles like this:

 

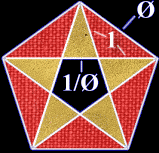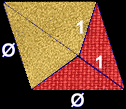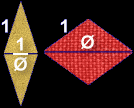The ratio of the two types of tiles in the resulting patterns is always phi!

As you expand the tiling to cover greater areas, the ratio of the quantity of the one type of tile to the other always approaches phi, or 1.6180339…, the Golden Ratio.

Within this tiling there can be small areas of five-fold symmetry. Decagons can also occur, which when grouped together can look like pentagons from a distance.

Explore further with these resources:

You can download a free program called “Bob” to generate Penrose tiling like the above at the site of Stephen Collins.

You can buy acrylic puzzles of Penrose darts, kites and tiles and other pentagon-based shapes at Kadon Enterprises.

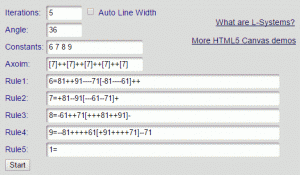
Create Penrose tiling with an L-System fractal generator. (See more on L-System) The input variables shown on the left create the pattern on the right. Note that the 36 degree angle is based on 360 degrees divided by 5 and then by 2, which relates it to the five-sided symmetry of Penrose tiling.

Quasi-Crystals

Phi also gives 5-fold symmetry in 3D with a single shape, known as a quasi-crystal.

Phi is intrinsically related to the number 5

The appearance of the golden ratio in examples of five-fold symmetry occurs because phi itself is intrinsically related to the number 5, mathematically and trigonometrically.

• A 360 degree circle divided into five equal sections produces a 72 degree angle, and the cosine of 72 degrees is 0.3090169944, which is exactly one half of phi, the reciprocal of Phi, or 0.6180339887.

• Phi itself is computed using the square root of five, as follows:

5 ^ .5 * .5 + .5 = Phi

In this mathematical construction, “5 ^ .5” means “5 raised to the 1/2 power,” which is the square root of 5, which is then multiplied by .5 and to which .5 is then added.  See more on the Five and Phi page.