The number 5 is intrinsically related to Phi and the Fibonacci series.
Phi can be derived from several formulas based on the number 5. The most traditional, based on the geometric construction of phi is this:
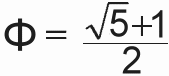
This formula for phi can also be expressed all in fives as:
Φ = 5 ^ .5 * .5 + .5
Another formula for phi based entirely on 5’s, an original insight contributed by Erol Karazincir (pcerol@yahoo.com), is as follows:
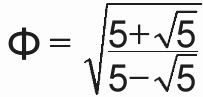
And, as pointed out by W. Nathan Saunders, the terms in above representation of phi can be expressed in yet another way that involves four 5’s:
(5 + √5) x (5 – √5) = 5 + 5 + 5 + 5
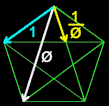
Phi appears in the geometry of the 5-sided pentagon
Take a pentagon with 5 equal sides and connect all the points to form a 5-pointed star. The ratios of the lengths of the resulting line segments are all based on phi.
Phi appears in the natural logs and trigonmetric functions
Phi can be related to e, the base of natural logs,
through the inverse hyperbolic sine function:
Phi = e ^ asinh(.5)
Determining the nth number of the Fibonacci series
You can compute the nth number in the Fibonacci series (fn) using phi and root 5:
fn = Phi n / 5½
5 is the 5th Fibonacci number
5 is also the 5th of the Fibonacci numbers, including 0, 1, 2, 3, and 5.
5 appears in the human body, which has proportions based on phi
 Another interesting aspect of phi and five is in relation to the design of the human body, which in addition to being based on phi relationships in its proportions, has:
Another interesting aspect of phi and five is in relation to the design of the human body, which in addition to being based on phi relationships in its proportions, has:
- 5 appendages from the torso, in the two arms, two legs and a head,
- 5 appendages on each of legs and arms in the five fingers and five toes,
- 5 openings on the face, and
- 5 senses in sight, sound, touch, taste and smell.
5 deserves a “high 5” for its role in phi, don’t you think!




Remember the 24 pattern?
its a 12-12 right?
5 appears again in a DODECAHEDRON, where this 12-sided polyhedron has each face being a pentagon 🙂
5 = PHIve.
5 = five = PHIve which is phi + v + e.. The letter V is the roman numeral for five and the letter E is the fifth letter of the roman alphabet. Coincidence?!
(5 + sqrt(5)) * (5 – sqrt(5)) != 25
Try √((A2+A3)/(A2-A3)) where A2=5 AND A3=√(5).
THIS WORKS FOR ME!
BUT I couldn’t make any sense of
(5 + √5) x (5 – √5) = 5 + 5 + 5 + 5 so what?
It’s just another way to express four fives in a relationship, although admittedly not one that represents Phi.
In a spreadsheet enter a column where the following formula is repeated (1+1/previous value)
Equations a column, e.., =1, =1+1/A1, =1+1/A2, …, =1+1/An
This will generate successive values converging in Phi, also note the Phi’s generated with by starting with any initial value (not 1). – Amazing.
In a spreadsheet enter a column where the following formula is repeated ( =Previous + Previous to that)
Fib Equation:=0, =1, =A2+A3, =A3+A4, =A4+A5, …, =A(n)+A(n-1)
(A1, A2 are inital values, enter other “seed” numbers (plus or minus) an see the results. Amazing.
In adjacent columns, calculate ratios
Equations For Smaller/Larger: =A3/A4, =A4/A5, =A5/A6, …, =A(n-1)/A(n)
Equations For Larger/Smaller: =A4/A3, =A5/A4, =A6/A5, …, =A(n)/A(n-1)
Ok so what is amazing?
These equations and relationships are just the sort that would find application in nature.
The interactive “one over plus one over” iteration represents the simplest version of the inverse proportion ratios (1/x) found in natural processed (forces?) and converging on natural replicated occurrence.
The ratio of Fibonacci numbers is also well represented in nature, but it is not the high nth iteration of these that have relevance, it is the fact that they occur everywhere there is life and replicated and differentiated in evolution.
Every fifth Fibonacci Sequence number is divisible by 5 also;
10th : 55 = 5 x 11
15th : 610 = 5 x 122
20th : 6765 = 5 x 1353
etc…
🙂
(P.S this also re-creates a new 24 digital root pattern in both the 5th Fib numbers sequence and the amounts that is divisible into it.)
It depends where the starting point is as most people start with 1 but the 1st Fibonacci number is 0. It’s up for interpretation really but makes for sense to start 0 1 … 0+1=1 1+1=2 and so on. Either way I’m just being pedantic and you are still right haha!
diatomic
Pi x phi = 5.08309262
5, 8 of fibonacci
Powers of phi can be expressed as the midpoint formula between two separate functions, both of which follow the Fibonacci sequence rule of adding the two previous values to get the next value.
Phi^3 = (4 + 2xsqrt(5))/2 ; Phi^2 = (3 + 1xsqrt(5))/2 ; Phi^1 = (1 + 1xsqrt(5))/2 ; Phi^0 = (2 + 0xsqrt(5))/2 ;
Phi^-1 = (-1 + 1xsqrt(5))/2 ; Phi^-2 = (3 – 1xsqrt(5))/2 ; Phi^-3 = (-4 + 2xsqrt(5))/2…
The two patterns can be seen to be whole numbers (of the Lucas number set, -11, 7, -4, 3, -1, 2, 1, 3, 4, 7, 11…) and the square root of 5 multiple numbers (of the recognizable Fibonacci sequence), of which each set contains alternating members of two specific functions relating to Phi.
Y = (0.5sqrt(5)+0.5)^X+(0,5sqrt(5)+0.5)^-X ; Y = (0.5sqrt(5)+0.5)^X-(0.5sqrt(5)+0.5)^-X
These two functions are as similar to e as hyperbolic cosine and sine functions (respectively), in that it is a power function split into a function similar to y=x^2, and a function similar to x^3, both of which add to make the function itself.
It is important to note, however, hyperbolic cosine and sine are 1/2 the difference between their power difference functions, so adding sinh(x) to cosh(x) gives e^x instead of 2e^x.
So the functions represented by the parts given relate exactly to the values including the 2 in the denominator, if functions similar to hyperbolic cosine and sine but relating to phi^x instead, the functions as given above would need to be halved.
Y =0.5 ((0.5sqrt(5)+0.5)^X+(0,5sqrt(5)+0.5)^-X) ; Y =0.5 ((0.5sqrt(5)+0.5)^X-(0,5sqrt(5)+0.5)^-X) or
Y = (Phi^x+Phi^-x)/2 and Y = (Phi^x-Phi^-x)/2
This gives legitimacy as to why the fibonacci numbers in negative powers alternate between positive and negative values.
take a pentagon, then put all the lines in from each corner, that makes a new pentagon in the middle.
use that pentagon and mirror of each side of the pentagon and your big pentagon is almost full
repeat the same with every pentagon you have, then do it again and again and again, well I wnet to 6 levels, but it is infinite.
you still have the big pentagon but inside that a very beautiful pattern with all the gaps develops.
guess what in these gaps you can fill up with more pentagons of sizes you already have.
keep going and going till it is almost full. you have tiny diamonds left in the pattern.
Phi can also be ((5^.5)+2)^(1/3)
Very true! The unique mathematical property in this is that the cube of Phi is the square root of 5 plus 2:
Root 5 = 2.236…
2.236… + 2 = 4.236…
Phi cubed = 4.236